All Weather Portfolio – Risk Parity (Example Portfolios + Coding Example)

Traders and investors are always searching for strategies that can withstand the test of time and provide consistent returns, irrespective of economic conditions.

One such approach is the All Weather Portfolio, a risk parity strategy designed to achieve well-balanced asset allocation and optimize risk-adjusted returns.

The term All Weather is derived from the idea that no matter what the economy is doing the portfolio is structured in a way such that it can perform well and not suffer big hits.

This article looks into the fundamentals of the All Weather Portfolio, discussing its basic building blocks, optimal beta and alpha portfolios, and example asset allocation mixes for a robust investment strategy.

Key Takeaways – All Weather Portfolio (Risk Parity)

• The All Weather Portfolio is a risk parity strategy that aims to achieve a well-balanced asset allocation free of biases to changes in discounted conditions and to optimize risk-adjusted returns.
• The portfolio rests upon three basic building blocks: risk-free return, returns from beta, and returns from alpha.
• The optimal beta portfolio is an essential element that achieves broad diversification across various asset classes and risk factors.
• Constructing an All Weather Portfolio lies in the right asset allocation mix, comprising a well-diversified combination of stocks, bonds, commodities, and other alternative investments to achieve a resilient portfolio that can perform well in both favorable and unfavorable economic conditions.

Basic Building Blocks

The All Weather Portfolio strategy rests upon three basic building blocks:

• risk-free return
• returns from beta, and
• returns from alpha

Risk-Free Return

The risk-free return is the return on an investment with virtually no risk, typically represented by treasury bonds or cash.

Beta

Beta returns refer to the returns generated by a portfolio’s exposure to systematic risks, such as market fluctuations.

Alpha

Alpha returns, on the other hand, are the excess returns earned by a portfolio through active management or skill, independent of overall market performance.

Risk parity is most commonly a beta product, where it is a strategic asset allocation mix and not a tactical asset allocation mix intended to generate alpha (from tactical decisions).

However, there are many flavors.

The combination of these three components lays the foundation for the All Weather Portfolio, with the ultimate goal of generating consistent returns across all economic scenarios, while minimizing the impact of market volatility.

Optimal Beta Portfolio

The Optimal Beta Portfolio (what some might call smart beta, as derived from Modern Portfolio Theory) is an essential element of the All Weather Portfolio, as it aims to achieve broad diversification across various asset classes and risk factors.

In this approach, investors allocate their capital to different assets based on their risk contribution, rather than their expected return.

This results in a more balanced portfolio, where each asset contributes an equal amount of risk, helping to minimize the overall portfolio volatility and protect against market downturns.

“All Weather” Asset Allocation Mix

The key to constructing an All Weather Portfolio lies in the right asset allocation mix, which should comprise a well-diversified combination of stocks, bonds, commodities, and other alternative investments.

The idea is to balance exposure to growth assets, such as equities, with defensive assets, like bonds, to achieve a resilient portfolio that can perform well in both favorable and unfavorable economic conditions.

Typically, the All Weather Portfolio includes a larger allocation to bonds, particularly long-term government bonds, which tend to perform well during economic downturns.

The bond side is often leveraged to match the risk of pro-growth assets like equities, often through things like futures, which require small capital outlay relative to the exposure taken on.

Equities, commodities, and other assets are also included in the mix to benefit from growth opportunities during periods of economic expansion.

Risk Parity & the Concept of Environmental Bias

In a risk parity framework, combining discounted growth and inflation scenarios results in four distinct economic environments:

• high growth with low inflation
• low growth with low inflation
• high growth with high inflation, and
• low growth with high inflation

Each of these environments has implications for different asset classes.

Below is an overview of each scenario and the suitable asset allocation for them:

Example Risk Parity Portfolio Allocations

Below we give some example All Weather risk parity allocations.

Please note that these are just examples and not recommendations (which should be personalized to your goals, time horizon, and risk tolerance).

Example #1

These allocations can be done with cash securities or done with other instruments like futures contracts.

Professional managers will often use things like futures for things like gold to avoid tying up a lot of cash in the asset.

This avoids taking away from the core assets in the portfolio. (This approach is often called an “overlay.”)

Example #3 (Ray Dalio Allocation)

An example from Ray Dalio:

• Stocks (30%):
  • US Equities: 15%
  • International Equities: 15%
• Bonds (55%):
  • Long-term Government Bonds: 40%
  • Intermediate-term Government Bonds: 15%
• Commodities (7.5%):
  • Diversified commodities: 7.5%
• Gold (7.5%):
  • Physical gold or gold ETFs (or via futures): 7.5%

Example #4

Now let’s say we wanted to take the above example and be a bit more precise about how we want to diversify.

For example, we might say we want more international exposure for geographic and currency diversification, as well as more diversification in the bond mix.

So we include more international exposure as well as more inflation-linked bonds:

• Equities (40%):
  • US Equities: 20%
  • European Equities: 10%
  • Emerging Market Equities: 10%
• Nominal Government Bonds (20%):
  • US Treasury Bonds (Intermediate-term): 10%
  • German Bunds (Intermediate-term): 10%
• Inflation-Linked Bonds (25%):
  • US TIPS (Treasury Inflation-Protected Securities): 15%
  • UK Index-Linked Gilts: 10%
• Commodities (7.5%):
  • Broad-based Commodity Index Fund: 7.5%
• Gold (7.5%):
  • Physical gold, gold ETFs, or futures: 7.5%

In the article we link below, we found that in these types of simple risk parity allocations, testing from data from 1972 forward, the “optimal” allocation – i.e., best Sharpe or Sortino ratio – is around:

• 35-40% Stocks
• 30-40% Bonds
• 15-20% Gold
• 5-15% Cash

Related: 3- and 4-Asset Portfolios

Example #5

Here we’ll give a more detailed breakdown with example ETFs.

Note that DM = developed markets (e.g., US, Canada, Western Europe, Australia) and EM = emerging markets.

• 25% DM Stocks (e.g., VTI)
• 5% EM Stocks (e.g., VWO)
• 5% DM Corporate Bonds (e.g., VTC)
• 5% DM Government Bonds (e.g., BND)
• 5% EM Bonds in USD (e.g., VWOB)
• 5% EM Bonds in Local Currency (e.g., EMLC)
• 25% Inflation-Linked Bonds (e.g., TIP)
• 5% Commodities (e.g., GSG)
• 15% Gold (e.g., GLD or IAU)
• 5% Cash

Alternatives & Private Assets in a Risk Parity Portfolio

Incorporating alternatives – like private assets (private equity, real estate, infrastructure, etc.) – into a risk parity portfolio requires considering their unique risk-return characteristics and how they correlate with traditional asset classes.

These private assets often offer diversification benefits due to their ostensibly lower correlation with public markets – or at least directly provide income rather than reliance on asset appreciation.

This can enhance portfolio resilience.

Private assets can provide higher return potential but also come with higher risk, limited liquidity, and longer investment horizons.

In a risk parity framework, you should assess the volatility and risk contribution of these assets relative to other components.

Because private assets often have different risk profiles and liquidity terms compared to public equities or bonds, their inclusion should be carefully calibrated to maintain the overall risk balance of the portfolio.

It’s important to use appropriate leverage and rebalancing strategies, as the illiquidity of private assets can complicate these processes.

Moreover, due to valuation complexities and infrequent pricing, estimating the true market risk of private assets can be challenging.

This requires a more nuanced approach to risk assessment and portfolio construction.

What is risk parity? | FT Markets

Optimal Alpha Portfolio

The Optimal Alpha Portfolio focuses on generating excess returns by exploiting market inefficiencies, active management, and skillful investment selection.

In the context of the All Weather Portfolio, incorporating an alpha component can help enhance the overall returns while maintaining a balanced risk profile.

To achieve this, traders/investors may include strategies such as tactical asset allocation, security selection, or the use of alternative investments, such as hedge funds or private equity.

As an example, a trader will tilt the equities portion of the portfolio toward a certain sector to better align with personal preferences or better balance the equity allocation in light of other goals.

For instance, tilting the stock portion toward consumer staples relative to what an index (e.g., S&P 500) might offer.

Alpha is generally less important in risk parity strategies.

Generally, alpha is done as an overlay for clients who want this approach.

In general, alpha overlay involves making tactical bets within a risk parity framework.

So, alpha within the context of a risk parity portfolio follows the idea of tactical bets or tilts within the basic structure and diversification principles of risk parity.

Alpha Overlay and Portable Alpha

Alpha overlay and portable alpha are advanced investment/trading strategies that can complement a risk parity portfolio.

Let’s look at these concepts and how they can be integrated within the context of a risk parity structure.

Alpha Overlay

Alpha overlay refers to the application of active investment strategies or decisions on top of an existing portfolio.

It aims to generate excess returns (alpha) independent of the underlying market movements.

This involves using derivatives or other instruments to gain exposure to desired strategies without altering the underlying asset allocation.

Application in Risk Parity

In a risk parity portfolio (primarily beta-focused and designed for balanced risk distribution), an alpha overlay can add a layer of active management aimed at generating additional returns.

It allows the portfolio to maintain its risk parity structure while seeking to exploit market inefficiencies or other opportunities identified by the overlay strategy.

Common alpha overlay strategies include currency hedging, individual stock selection, or sector rotation.

It can be implemented through derivatives like futures, options, or swaps.

Portable Alpha

Portable alpha is a strategy where traders/investors separate the alpha (market outperformance) from a specific investment and “port” or apply it to another asset or portfolio.

Essentially, it involves creating returns independent of the traditional risk-return profile of the asset classes in the portfolio.

Application in Risk Parity

In a risk parity framework, portable alpha can be used to enhance the overall return of the portfolio without disturbing the underlying risk balance.

This might involve, for example, borrowing against low-risk assets in the risk parity portfolio (e.g., low-interest cash) to invest in alpha strategies.

The alpha generated from these investments is then “ported” back to the risk parity portfolio.

Portable alpha strategies might include investing in hedge funds, private equity, or other alternative investments that are expected to generate returns uncorrelated with the main asset classes (“betas”) in the risk parity portfolio.

Integrating Alpha Overlay and Portable Alpha with Risk Parity

Maintaining Risk Balance

Care must be taken to ensure that the alpha strategies do not significantly alter the risk parity structure.

The risk introduced by the alpha strategies should be independently managed and hedged if necessary.

Consideration of Correlations

It’s important to understand how the returns from the alpha strategies correlate with the existing assets in the risk parity portfolio.

The goal to achieve true alpha means returns that are uncorrelated with the broader market.

Use of Derivatives and Leverage

Both alpha overlay and portable alpha often involve the use of derivatives and leverage.

It’s important to manage these tools carefully to avoid introducing unintended risk exposures.

Costs and Complexity

These strategies add layers of complexity and can incur additional costs (like borrowing costs for leverage or fees for external managers).

These should be weighed against the potential benefits.

Continuous Monitoring and Adjustment

Given the dynamic nature of alpha strategies, continuous monitoring and periodic adjustment are necessary to align with the overall portfolio objectives and risk parameters.

Mathematical Foundations of Risk Parity

Risk parity is based on the observation that in a traditional portfolio, asset classes with higher volatility tend to have a disproportionate impact on the portfolio risk profile.

The goal of risk parity is to construct a portfolio where each asset contributes equally to the overall risk of the portfolio.

The mathematical foundations of risk parity involve several key concepts from quantitative finance:

Volatility and Risk Measurement

Risk parity relies on measures of risk such as volatility.

This is often quantified using the standard deviation of asset returns.

Or other risk metrics like Value at Risk (VaR) or Conditional Value at Risk (CVaR).

These measures are used to understand the distribution and magnitude of potential losses.

Correlation

The correlation coefficient measures the degree to which two assets move in relation to each other.

In a risk parity portfolio, it’s important to analyze the correlations between assets to ensure that risk is not concentrated in assets that tend to move in the same direction.

Also, correlation is not necessarily designed to be based on backward-looking data.

Correlations change over time.

So it’s more fundamentally about what assets are intrinsically like.

For example, stocks and bonds are not inherently negatively correlated.

They may be in a macro environment where inflation is steady and changes in discounted growth is the primary driver of asset price movements.

However, when inflation volatility picks up, stocks and bonds can have a positive correlation.

Leverage

To equalize risk contribution across assets with different volatilities, risk parity portfolios often use leverage.

This is done by increasing the investment in lower-risk assets through borrowing, to amplify their contribution to the portfolio’s risk to be on par with higher-risk assets.

Optimization

The allocation of capital in a risk parity portfolio is determined through an optimization process that aims to equalize the risk contribution of each asset class.

This involves solving for the portfolio weights w that minimize the portfolio variance σ^2, subject to the constraint that the risk contributions are equal.

Mathematically, this can be represented by the function to minimize:

min(w^T*Σw)

Subject to:

RCi = wi * (∑w)i = 1/N ∑RCi

Where:

• Σ is the covariance matrix of the asset returns,
• wi is the weight of the i-th asset, and
• RCi is the risk contribution of the i-th asset.

Covariance Matrix

The covariance matrix Σ is central to the optimization process as it contains the variances and covariances of all asset pairs.

Risk parity strategies require a stable and robust estimation of covariances.

This is often challenging due to the dynamic nature of financial markets.

Risk Budgeting

Risk budgeting is an approach that assigns a certain “budget” of risk (rather than capital) to each asset or asset class based on its risk profile.

In the context of risk parity, each asset’s risk budget is equal, and the portfolio’s asset weights are determined accordingly.

Numerical Methods

The optimization problem in risk parity is typically solved using numerical methods such as the Newton-Raphson method or other algorithms suitable for quadratic programming.

Summary

Risk parity portfolios are designed to perform well across different market environments by not being overly reliant on any single asset class.

This approach does not necessarily target the highest returns but rather seeks a balance between risk and return.

The central goal is to achieve more consistent performance over time.

Risk Parity Python Coding Example

Let’s say we have a simple 4-asset risk parity portfolio:

• Stocks
• Bonds
• Gold
• Commodities

And let’s say we want gold to be 15% of the portfolio and commodities to be 5% of the portfolio.

To determine the weights of stocks and bonds in a risk parity framework using coding/math, we first need to acknowledge the constraints given for commodities and gold.

These constraints set fixed portfolio weights for these two asset classes.

Our task is then to allocate the remaining portfolio weight between stocks and bonds in a way that equalizes their risk contributions with those of commodities and gold.

Step 1: Define Risk Contributions

The risk contribution of an asset is typically calculated as its weight multiplied by its risk (volatility in this case).

In a risk parity framework, we aim to equalize the risk contributions of all assets.

Step 2: Given Data

• Stocks: Forward return = 6%, Volatility = 15%
• Bonds: Forward return = 4%, Volatility = 10%
• Commodities: Forward return = 3%, Volatility = 15%, Weight = 5%
• Gold: Forward return = 3%, Volatility = 15%, Weight = 15%

Step 3: Initial Constraints

• Total weight of Commodities and Gold = 5% + 15% = 20%
• Remaining weight for Stocks and Bonds = 100% – 20% = 80%

Step 4: Formulate the Problem

We want to find the weights of stocks and bonds such that their risk contributions are in line with those of commodities and gold.

This is a constrained optimization problem.

Step 5: Optimization

The objective is to minimize the difference in risk contributions.

Let ws and wb be the weights for stocks and bonds respectively.

The risk contributions for each asset are:

• Stocks: ws * 0.15
• Bonds: wb * 0.10
• Commodities: 0.05 * 0.15
• Gold: 0.15 * 0.15

Given that the total weight for stocks and bonds is 80%, ws + wb = 0.80

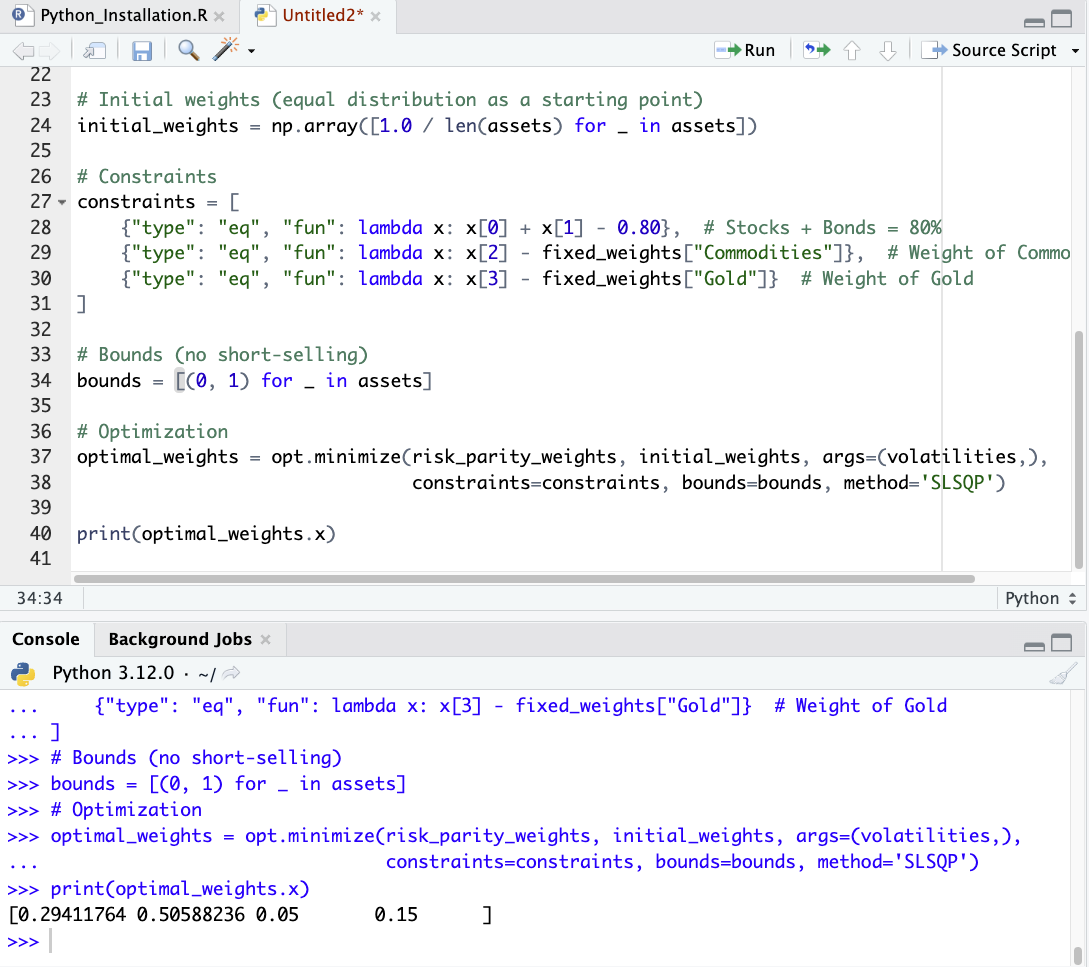
We can solve this using Python:

import numpy as np
import scipy.optimize as opt

# Asset characteristics
assets = {
"Stocks": {"return": 0.06, "volatility": 0.15},
"Bonds": {"return": 0.04, "volatility": 0.10},
"Commodities": {"return": 0.03, "volatility": 0.15},
"Gold": {"return": 0.03, "volatility": 0.15}
}

# Predefined weights for Commodities and Gold
fixed_weights = {"Commodities": 0.05, "Gold": 0.15}

# Risk parity function
def risk_parity_weights(weights, volatilities):
portfolio_risk_contributions = np.multiply(weights, volatilities)
return np.sum((portfolio_risk_contributions[:, None] - portfolio_risk_contributions[None, :])**2)

# Extracting volatilities
volatilities = np.array([assets[asset]["volatility"] for asset in assets])

# Initial weights (equal distribution as a starting point)
initial_weights = np.array([1.0 / len(assets) for _ in assets])

# Constraints
constraints = [
{"type": "eq", "fun": lambda x: x[0] + x[1] - 0.80}, # Stocks + Bonds = 80%
{"type": "eq", "fun": lambda x: x[2] - fixed_weights["Commodities"]}, # Weight of Commodities
{"type": "eq", "fun": lambda x: x[3] - fixed_weights["Gold"]} # Weight of Gold
]

# Bounds (no short-selling)
bounds = [(0, 1) for _ in assets]

# Optimization
optimal_weights = opt.minimize(risk_parity_weights, initial_weights, args=(volatilities,),
constraints=constraints, bounds=bounds, method='SLSQP')

print(optimal_weights.x)

This code will provide the optimized weights for stocks and bonds that align with the risk parity approach, given the fixed allocations to commodities and gold.

From this, we see optimal weights, given the characteristics presented, of:

• Stocks = 29.4%
• Bonds = 50.6%
• Gold = 15%
• Commodities = 5%

We can see these weights shown in the image below:

Other Concepts & Ways of Thinking About Risk Parity

Dynamic Risk Adjustment

Traditional risk parity strategies often use static risk contributions from different asset classes.

A different approach would be to dynamically adjust the risk contribution of each asset class so they provide the desired risk level.

Risk parity often involves using leverage to equalize the risk contributions of lower-risk assets (like bonds) to match those of higher-risk assets (like equities).

Assets that are too risky as they come prepackaged can also have their risk lowered by holding cash against them.

This process requires careful calibration to avoid excessive leverage

Incorporating Alternative Data

Use alternative data sources, like sentiment analysis from social media, economic indicators, or geopolitical events, to better understand and predict risk factors affecting asset classes.

This data can be integrated into the risk parity model to adjust allocations in response to emerging risks.

Tail Risk Hedging

Incorporating tail risk hedging strategies within a risk parity framework (tail risk parity) can provide additional protection against extreme market movements, which are often not adequately addressed by traditional risk parity models.

This can involve using derivatives, like options, to hedge against significant downside risks in the portfolio.

Diversification can also thin out the tails of one’s distributions (both on the downside, most importantly, but also on the upside).

ESG Integration

Incorporating Environmental, Social, and Governance (ESG) factors into the risk assessment process.

Some dismiss ESG, but it essentially just factors in other dimensions of risk that are niched down beyond the traditional high-level macroeconomic scope.

This approach recognizes that ESG issues can have significant impacts on long-term risk and returns, and therefore, could be factored into the risk parity strategy.

Leverage and Derivatives

Using leverage to balance the risk contributions from different asset classes, especially those with historically lower risk and return profiles.

Derivatives can also be employed to achieve more tailored exposure without significantly altering the capital allocation.

Multi-Factor Integration

Beyond just asset classes, risk parity strategies can be expanded to balance risk across multiple factors like size, value, momentum, etc.

This requires a deep understanding of how these factors interact and contribute to overall portfolio risk.

Global Diversification

Expanding the investment universe to include global assets, rather than just domestic ones.

This includes emerging market equities and bonds, global real estate, and commodities, which can provide additional diversification benefits.

This also includes different currency exposures and brings another element (which may be wanted to a degree, but too much of a portfolio’s return based on FX may be unacceptable).

Liquidity Considerations

Incorporating liquidity risk into the risk parity framework.

This involves understanding the liquidity profile of different asset classes and adjusting allocations based on the ease of entering and exiting positions.

Stress Testing and Scenario Analysis

Regularly conducting stress tests and scenario analyses to understand how the risk parity portfolio would perform under different market conditions, including financial crises and other extreme events.

Correlation and Covariance Analysis

Understanding the correlation and covariance among different asset classes is important.

This analysis helps in determining how assets interact under various market conditions.

It’s used in constructing a diversified portfolio that balances risk across assets.

Correlation Dynamics and Conditional Correlations

Recognizing that correlations between assets are not static and can change, especially during market stress.

Implementing dynamic correlation models (e.g., DCC-GARCH) are one way algorithmic risk parity traders adjust the portfolio as correlations change over time.

Risk Decomposition and Contribution Analysis

Decomposing the total portfolio risk into contributions from each asset or asset class. This involves understanding how much each asset contributes to the overall portfolio volatility.

Using techniques like variance decomposition, one can calculate the marginal contribution to risk (MCTR) for each asset.

This way, each contributes equally to the portfolio’s risk in the desired way.

Volatility Forecasting

Risk parity strategies often depend on forecasting the volatility of different asset classes.

This can involve complex statistical models, which are used to model and predict changing volatility over time.

This improved forecasting can enhance the risk allocation process in risk parity portfolios.

Behavioral Finance Insights

Applying insights from behavioral finance to understand and predict investor behavior.

This can have a big impact on market dynamics and, consequently, on the risk profiles of different asset classes.

For example, in developed market economies it’s been rare to see very low growth simultaneously with high inflation.

We don’t have a lot of historical data for some circumstances, so how would traders and investors react to such an environment?

Most portfolios, because they’re optimized on the past, aren’t prepared for that, and the equity- and nominal bonds-centric portfolio approach generally does poorly in such scenarios.

This can also involve strategies to mitigate the impact of herd behavior, overreaction to market news, etc.

Macroeconomic Modeling

The effectiveness of risk parity is often tied to underlying economic regimes.

By understanding the dynamics of macroeconomic shifts, such as transitions from inflationary to deflationary periods or from economic expansion to contraction, traders can better adapt risk parity portfolios to changing market conditions.

Incorporating macroeconomic models to understand and predict changes in economic conditions that could affect asset class performance, such as interest rate changes, inflation, GDP growth, etc.

But gets more into the alpha-generation aspect of risk parity.

Machine Learning and AI in Risk Parity

As portfolio construction becomes more modern, machine learning and AI techniques are used to improve the prediction of market dynamics and optimize portfolio construction and risk balancing strategies.

Role of Alternative Assets

Examining the role of alternative assets (like hedge funds, private equity, private credit, real estate) in risk parity portfolios offers unique perspectives.

These assets can have different risk-return profiles and may behave differently across economic cycles compared to traditional assets.

Impact of Globalization

Understanding how globalization affects asset classes differently can enhance risk parity strategies.

For instance, the interconnectedness of global markets may lead to changing correlations between domestic and international assets.

Non-Normality of Returns and Higher Moments

Recognizing that asset returns are generally not normally distributed and will exhibit skewness and kurtosis.

Incorporating higher moments of return distributions into risk assessment.

This moves beyond standard deviation as the sole measure of risk.

Multi-Level Risk Parity

Applying risk parity not just at the asset class level but also within asset classes.

This involves constructing a portfolio where risk parity is achieved both across and within asset classes, such as different types of equities or bonds.

For example, an investor/trader might want China to be 5-10% of its portfolio.

One could design a risk parity portfolio that has the same characteristics as a US or developed market based one, but just with Chinese assets and China as one piece of the broader portfolio.

Complex Systems Theory

Financial markets can be viewed through the lens of complex systems theory.

This perspective considers markets as adaptive systems with emergent properties, influenced by the interactions of various components (like different asset classes).

Understanding these interactions is used in managing the systemic risks in risk parity portfolios.

Network Theory in Financial Markets

Applying network theory to understand how different assets are interconnected can offer insights into how shocks can propagate through a portfolio and impact a risk parity strategy.

Options in Risk Parity

The use of options in a risk parity portfolio can be an effective way to manage and control risk.

In basic risk parity portfolios, it’s generally just allocations to cash assets.

Options provide unique advantages due to their non-linear payoff structures and can be used to hedge specific risks or to enhance returns while maintaining the overall risk balance of the portfolio.

Here’s an explanation of how options can be used in risk parity, along with some unique options strategies:

Use of Options in Risk Parity

Tail Risk Hedging

Options are often used in risk parity portfolios for tail risk hedging.

Purchasing out-of-the-money (OTM) put options on equities can protect against significant market downturns.

This strategy ensures that the portfolio is insulated from extreme negative events and maintain the desired risk equilibrium.

Controlling Volatility

Options can be employed to control the overall volatility of the portfolio.

By using strategies like covered calls or protective puts, the portfolio’s risk profile can be adjusted.

For instance, writing covered calls on equities can generate income and reduce volatility.

Dynamic Risk Adjustment

Options allow for dynamic risk adjustment.

As market conditions change, options can be used to quickly alter the risk exposure of the portfolio without needing to significantly rebalance the underlying assets.

There are concepts like calculating the delta of the options to understand the hedge ratio required to achieve neutrality or a specific directional bias.

Considerations

• Cost: Options strategies can incur significant costs, including premiums and transaction fees.
• Complexity: Managing options requires a deep understanding of derivatives and their pricing, as well as ongoing monitoring.
• Liquidity Risks: Some options strategies may involve instruments that lack liquidity, which can pose additional risks.
• Integrating with Broader Portfolio: The options strategy should be integrated with the broader portfolio in a manner that aligns with the overall investment objectives and risk parity principles.

Hedging in Risk Parity Portfolio

in risk parity strategies, enhancing their fundamental objective of balanced risk distribution across different asset classes.

Here’s an overview of how hedging is used within a risk parity framework:

Purpose of Hedging

In a risk parity portfolio, hedging is employed to manage and mitigate specific risks.

This way, no single asset class disproportionately contributes to the overall portfolio risk.

The goal is to neutralize certain risks that might skew the balance of the portfolio, such as market risk, interest rate risk, currency risk, or inflation risk.

Types of Risks to Hedge

Market Risk

Hedging against downturns in equity or other volatile markets, often using derivatives like put options.

Interest Rate Risk

In fixed-income components, interest rate swaps or options can be used to mitigate the impact of rising interest rates.

Currency Risk

For international assets, currency forwards or options can be employed to protect against currency fluctuations.

Inflation Risk

Inflation-linked bonds or commodities futures can hedge against the risk of rising inflation eroding real returns.

Hedging Instruments

Options (Puts and Calls)

Provide asymmetric payoffs, which are ideal for hedging because they limit downside risk while allowing for upside potential.

Futures Contracts

Can be used to hedge against movements in interest rates, currencies, equity indexes, or commodity prices.

Swaps

Interest rate swaps, currency swaps, and total return swaps can effectively hedge various types of portfolio risks.

Dynamic Hedging

Risk parity portfolios often benefit from dynamic hedging strategies, where the hedge positions are adjusted in response to changing market conditions and portfolio rebalancing.

Dynamic hedging is relevant for managing delta risk in options positions.

Cost of Hedging

Hedging, especially using derivatives, incurs costs (such as premiums for options).

These costs must be weighed against the benefits of reduced risk exposure.

Effective hedging should improve the risk-adjusted return of the portfolio, even after accounting for the costs.

Tail Risk Hedging

Tail risk hedging is particularly important in risk parity portfolios to protect against rare but severe market events.

This often involves buying OTM put options or using other strategies that have payoffs during market crashes.

Liquidity Considerations

When implementing hedging strategies, liquidity of the hedging instruments matters.

This ensures that they can be adjusted or unwound without significant cost or slippage.

Risk Parity Optimization

Risk parity optimization involves constructing a portfolio in which all assets or asset classes contribute equally to overall risk.

This goal is achieved using various optimization techniques and algorithms.

Here’s an overview of some key methods used in risk parity portfolio construction:

1. Mean-Variance Optimization (MVO) Adaptation

Traditional MVO

This classic approach optimizes for the highest return for a given level of risk (variance), based on expected returns and the covariance matrix of asset returns.

Adaptation for Risk Parity

Modify MVO to minimize portfolio variance under the constraint that each asset’s risk contribution is equal.

This often involves ignoring expected return assumptions.

Instead it focuses on risk distribution.

But risk parity approaches differ and many forms do take risk premium considerations into account.

2. Quadratic Programming

Concept

A type of optimization model where the objective function is quadratic and the constraints are linear.

Application

Used to solve the risk parity problem by minimizing the portfolio variance subject to the constraint that each asset’s risk contribution is equal and other constraints like budget or leverage.

3. Growth and Inflation Neutrality

Asset Classification

Assets are categorized based on their sensitivity to economic growth and inflation.

For example, equities are generally sensitive to growth, while inflation-linked bonds are responsive to inflation.

Balancing

The portfolio is constructed to balance exposure to these economic factors.

This can involve using a combination of assets like equities, government bonds, inflation-linked bonds, commodities, and real estate.

4. Skewness and Kurtosis Considerations

Skewness

This measures the asymmetry of the return distribution.

A portfolio skewed too far in either direction can indicate a risk of asymmetric losses or gains.

Kurtosis

This measures the “tailedness” of the distribution.

High kurtosis indicates a higher risk of extreme returns (both positive and negative).

Incorporating Higher Moments

Advanced optimization techniques consider these higher moments of distributions.

This can involve using optimization models that go beyond the quadratic form of MVO.

Incorporates skewness and kurtosis to address the non-normality of asset returns.

5. Risk Parity and Risk Budgeting

Risk Contribution

Each asset’s contribution to overall portfolio risk is calculated.

Considers not just variance but also skewness and kurtosis.

Risk Budgeting

Allocate risk, not capital, to each asset based on its risk profile and economic exposure.

This involves assigning a “risk budget” to each asset or asset class.

Ensures that the portfolio is not overly exposed to any particular economic scenario.

6. Leverage Adjustment

Purpose

In risk parity, less volatile assets are often leveraged to equalize their risk contribution to that of more volatile assets.

Method

After determining the unleveraged risk parity weights, leverage is applied to scale up the entire portfolio to the desired level of risk.

7. Iterative Risk Parity Algorithms

Process

Start with an initial set of weights, calculate each asset’s risk contribution, and iteratively adjust the weights until the risk contributions are equalized.

Tools

Algorithms such as the Newton-Raphson method can be used to find the optimal weights that balance the risk contributions.

8. Use of Derivatives for Fine-Tuning

Strategy

Incorporating derivatives like futures, options, or swaps to fine-tune risk exposure and achieve the desired risk parity without significantly altering the underlying asset allocation.

9. Monte Carlo Simulations

Purpose

To assess the robustness of the risk parity portfolio under a range of market conditions.

Application

Simulating a wide variety of market scenarios to see how well the portfolio maintains its risk parity characteristics.

10. Heuristic Methods

Concept

Utilizing simpler, more intuitive methods for portfolio construction, like equal weighting or inverse volatility weighting, as a starting point for risk parity.

Refinement

Further adjusting these heuristic allocations using optimization techniques to achieve exact risk parity.

11. Dynamic Rebalancing Algorithms

Necessity

Risk parity portfolios require regular rebalancing to maintain equal risk contribution.

Approach

Implementing algorithms that trigger rebalancing based on predefined criteria, such as deviation from target risk contributions, time intervals, or the statistical properties of asset returns.

12. Stress Testing and Scenario Analysis

Simulating Extremes

Perform stress tests and scenario analyses to see how the portfolio would behave under extreme market conditions, including high inflation or low growth scenarios (where most portfolios notably struggle)

Adjusting for Tail Risk

Based on these analyses, adjust the portfolio to mitigate the effects of extreme events, potentially using tail risk hedging strategies.

13. Liquidity Considerations

Liquidity Risk

Factor in the liquidity of assets, as this affects the ability to adjust the portfolio in response to market changes.

FAQ – All Weather Portfolio (Risky Parity)

What makes the All Weather Portfolio different from other investment strategies?

The All Weather Portfolio strategy is designed to provide consistent returns and minimize volatility by maintaining a balanced risk profile.

It achieves this through a combination of risk-free returns, optimal beta and alpha portfolios, and a diversified asset allocation mix.

This approach enables the portfolio to perform well across various economic conditions, unlike some other strategies that may focus solely on maximizing returns or minimizing risk.

Such approaches that place the bulk of a portfolio in a certain asset class can be heavily unbalanced as result, running very hot or very cold depending on the environment.

What are the main factors that cause asset prices to change?

Asset prices are basically determined by four things:

• Changes in discounted growth
• Changes in discounted inflation
• Discount rates
• Risk premiums

All asset have an environmental bias.

Stocks do best during period of higher than expected growth and low to moderate inflation.

Nominal-rate reserve-currency government bonds do best when growth is below expectation and inflation is low.

Commodities tend to do best during inflationary growth periods (and are often partially the cause of the inflation itself).

Assets like gold do best when real interest rates fall due to its nature as an “inverse money” type of asset.

What assets should be included in a risk parity portfolio?

A risk parity portfolio attempts to balance exposure across various asset classes and countries:

• Equities: Provide growth potential with a mix of developed and emerging markets.
• Nominal Government Bonds: Offer stability in deflationary or low-growth environments.
• Inflation-Linked Bonds: Help protect against inflation, with allocations in both the US and the UK being the most common.
• Commodities & Gold: Serve as a hedge against inflation and currency depreciation.

How does the risk parity approach work in the All Weather Portfolio?

Risk parity is a core concept in the All Weather Portfolio strategy.

It focuses on allocating capital based on the risk contribution of each asset, rather than their expected return.

It is often known as “balanced beta” or a “balanced portfolio.”

There are also approaches such as VRP overlay.

By doing so, the portfolio achieves a more balanced risk profile, where each asset contributes roughly an equal amount of risk.

This helps to reduce overall portfolio volatility and protect against market downturns.

Can the All Weather Portfolio guarantee positive returns in all market conditions?

No. While the All Weather Portfolio is designed to perform well across various economic scenarios, it is important to remember that no investment strategy can guarantee positive returns in all market conditions.

The goal of the All Weather Portfolio is to optimize risk-adjusted returns and minimize volatility, but it does not eliminate the inherent risks associated with investing.

Is risk parity worth it?

Risk parity can be effective for diversification and managing volatility. But it’s complex and may not suit all investors.

Its worth depends on individual risk tolerance, investment goals, and market conditions.

How often should I rebalance my All Weather Portfolio?

Rebalancing your All Weather Portfolio is crucial to maintain the desired risk profile and asset allocation mix.

It is generally recommended to review and rebalance your portfolio at least once a year, or more frequently if there are significant market changes or shifts in your financial goals.

Can I implement the All Weather Portfolio strategy using low-cost index funds or ETFs?

Yes, you can implement the All Weather Portfolio strategy using low-cost index funds or ETFs that represent the various asset classes included in the strategy.

This approach can help to minimize fees and make it easier to manage your portfolio, while still benefiting from the risk parity and diversification principles of the All Weather Portfolio.

Is the All Weather Portfolio suitable for all types of investors?

The All Weather Portfolio strategy can be suitable for a wide range of investors, particularly those who are looking for a balanced approach to investing that prioritizes risk management and long-term, consistent returns.

However, individual investment objectives, risk tolerance, and time horizon should always be considered when determining if the All Weather Portfolio is the right or an appropriate strategy for you.

It is recommended to consult with a financial advisor to tailor the approach to your specific needs and goals.

Conclusion

The All Weather Portfolio is an effective investment strategy that seeks to optimize risk-adjusted returns by combining the basic building blocks of risk-free return, beta, and alpha returns, along with a well-balanced asset allocation mix.

Risk parity isn’t about eliminating risk but about understanding and balancing it more effectively.

By following this approach, traders/investors can create a resilient portfolio that can weather various economic conditions and deliver consistent performance over the long term.