Position Sizing

Position sizing refers to the technique of determining the appropriate amount of capital or number of shares to allocate for a specific trade or investment.
This process is important for several reasons:
- Risk Management – It helps in managing the risk associated with individual trades, such that losses don’t disproportionately affect the overall portfolio.
- Potential Return Optimization – By strategically allocating capital, traders can optimize their potential returns, balancing risk and reward effectively.
- Psychological Impact on Trading Decisions – The size of a position can affect a trader’s emotional state and influence decision-making under stress.
Key Takeaways – Position Sizing
Position Sizing Methods
Fixed Percentage Risk
This method involves limiting the risk on each trade to a predetermined percentage of the total capital, typically between 1% and 2%.
This is so that the amount at risk is proportional to the portfolio size.
Fixed Fractional
Here, investors purchase a set number of shares or units based on a fraction of their portfolio for each position.
This simplifies the allocation process.
Volatility-Based
This approach adjusts the position size according to the asset’s volatility.
This aims to normalize the risk across different investments.
For example, if a bond ETF had an expected volatility of 8% and a stock ETF had an expected vol of 16%, they’d allocated twice as much to bonds as stocks to keep the risk contribution between the two equal.
Related: Risk Parity
Kelly Criterion (Advanced)
The Kelly Criterion is a mathematical formula that calculates the optimal position size to maximize the long-term growth of the portfolio while controlling risk.
It requires an estimation of both the probability of winning and the win/loss ratio.
Related: Expected Value
Dollar-Based Risk
This involves setting a fixed dollar amount of risk per trade (e.g., $200).
This allows for larger positions in lower-priced stocks, and works well for traders focused on managing risk in absolute dollar terms.
Daily Stop-Loss Level
Day traders may set a maximum dollar loss they’re willing to incur in a single day.
If this amount is reached, they exit all positions for the rest of the day.
This limits overall daily risk exposure.
Specific Considerations
- Time Horizon – Since day trades are held for a short time, position sizing often focuses on managing intraday fluctuations rather than long-term trends.
- Liquidity – Day traders need to consider the liquidity of the assets they trade. Position sizes should be adjusted for less liquid securities to ensure they can be quickly exited if needed.
- Leverage – If using leverage in trading, position sizing becomes even more critical as both potential gains and losses are magnified.
Factors Influencing Position Size
Risk Tolerance
The investor’s individual comfort level with potential losses significantly influences position sizing.
Higher risk tolerance may lead to larger position sizes.
Goals
Objectives such as income generation, capital growth, or preservation dictate the approach to position sizing to align risk with desired outcomes.
Market Conditions
Current volatility, market trends, and overall sentiment can impact position sizing decisions.
Entry & Exit Points
The definition of clear stop-loss levels and profit targets is important for determining the amount of capital to risk on a trade.
Example of Position Sizing – Coding Example
To illustrate position sizing, let’s do an optimization of a portfolio using Monte Carlo simulation.
We can create a Python script that simulates numerous portfolio allocations across stocks, bonds, commodities, and gold, using a portfolio we’ve used as an example in other articles with these return and volatility assumptions.
- Stocks: +3-7% forward return, 15% annualized volatility using standard deviation
- Bonds: +1-5% forward return, 10% annualized volatility using standard deviation
- Commodities: +0-4% forward return, 15% annualized volatility using standard deviation
- Gold: +2-6% forward return, 15% annualized volatility using standard deviation
Our goal is to find an allocation that potentially offers the best risk-reward trade-off, characterized by the highest Sharpe ratio, under the given forward return and volatility assumptions.
Explanation
- Forward Returns Simulation – We simulate the expected return for each asset class within the given range to reflect the uncertainty in future returns.
- Volatility & Weights – We use the given volatilities and dynamically generated portfolio weights to calculate the portfolio’s overall volatility.
- Sharpe Ratio – This ratio helps us assess the risk-adjusted return of the portfolio, aiming for the highest value.
Let’s break down the steps and implement the simulation:
Define Portfolio Assumptions
Set the forward return range and annualized volatility for each asset class.
Generate Simulated Returns
For simplicity, we’ll randomly generate expected annual returns within the given ranges for each asset class.
Monte Carlo Simulation
Randomly sample portfolio weights, calculate portfolio returns and volatility, and determine the Sharpe ratio for each simulation.
Optimization Goal
Identify the portfolio allocation with the highest Sharpe ratio.
Here’s an example Python script to achieve this:
import numpy as np
# Portfolio assumptions
forward_returns = {
'Stocks': (0.03, 0.07),
'Bonds': (0.01, 0.05),
'Commodities': (0.00, 0.04),
'Gold': (0.02, 0.06)
}
volatility = {
'Stocks': 0.15,
'Bonds': 0.10,
'Commodities': 0.15,
'Gold': 0.15
}
# Number of portfolios to simulate
n_portfolios = 10000
# Risk-free rate assumption for Sharpe ratio calculation
risk_free_rate = 0.01
# Initialize arrays to store simulation results
all_weights = np.zeros((n_portfolios, len(forward_returns)))
ret_arr = np.zeros(n_portfolios)
vol_arr = np.zeros(n_portfolios)
sharpe_arr = np.zeros(n_portfolios)
# Monte Carlo simulation
for i in range(n_portfolios):
# Generate random weights
weights = np.random.random(len(forward_returns))
weights /= np.sum(weights)
all_weights[i, :] = weights
# Simulate expected return for the portfolio
simulated_returns = [np.random.uniform(low=low, high=high) for low, high in forward_returns.values()]
ret_arr[i] = np.sum(weights * simulated_returns)
# Calculate portfolio volatility
vol_arr[i] = np.sqrt(np.dot(weights.T, np.dot(np.diag(list(volatility.values())), weights)))
# Calculate Sharpe ratio
sharpe_arr[i] = (ret_arr[i] - risk_free_rate) / vol_arr[i]
# Find the portfolio with the highest Sharpe ratio
max_sharpe_idx = np.argmax(sharpe_arr)
optimal_weights = all_weights[max_sharpe_idx, :]
print(f"Optimal Portfolio Weights:\nStocks: {optimal_weights[0]:.2f}, Bonds: {optimal_weights[1]:.2f}, Commodities: {optimal_weights[2]:.2f}, Gold: {optimal_weights[3]:.2f}")
print(f"Maximum Sharpe Ratio: {sharpe_arr[max_sharpe_idx]:.2f}")
Results
Here’s the position sizing result from this code:
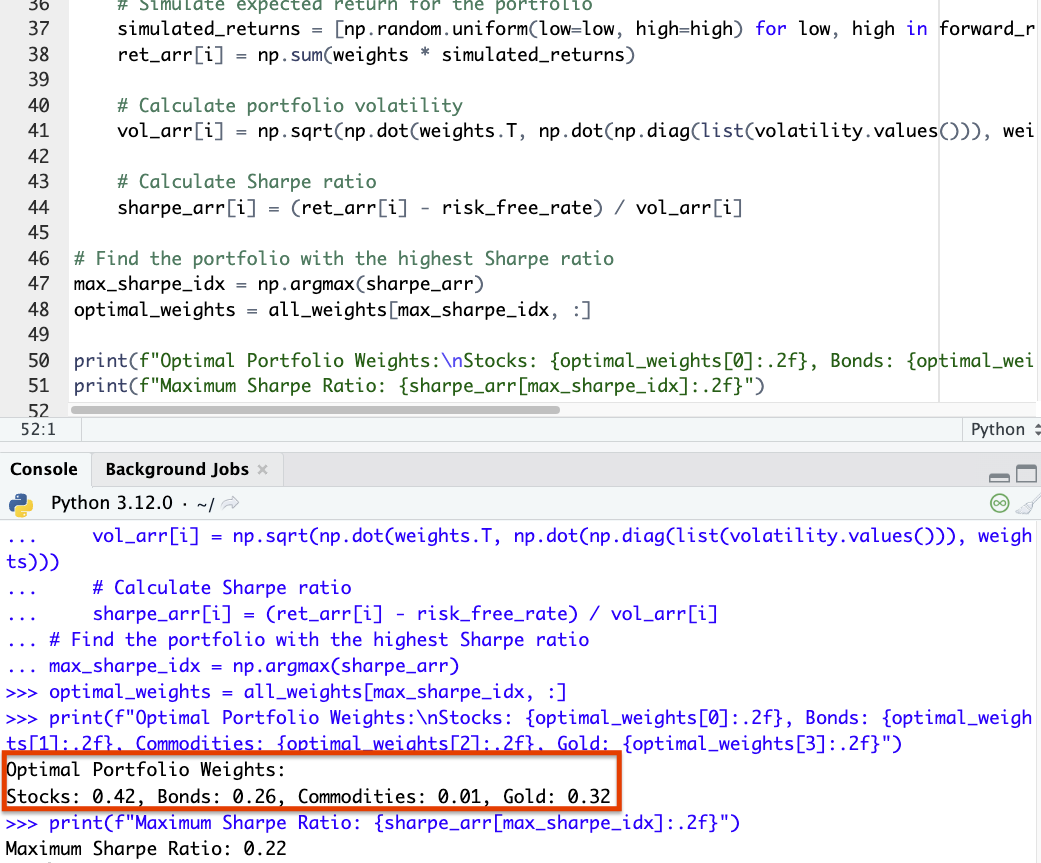
For strategic asset allocation purposes, the gold percentage is a bit high relative to what we’ve seen in backtesting.
But the general idea is that a trader could have certain position sizing considerations for a strategic asset allocation and tactically make deviations based on the opportunities they see.
Note
The Monte Carlo simulation approach used here is basic and serves as an illustrative example.
More sophisticated models might incorporate covariance between asset classes, more precise distributions of expected returns, and other constraints like maximum and minimum allocation limits to each asset class.
Advanced Considerations
Correlated Assets
Holding multiple positions in assets that are correlated increases overall portfolio risk.
Considering these correlations when sizing positions is important to avoid amplified losses.
Portfolio-Level Position Sizing
Beyond individual trades, managing risk and allocation across the entire portfolio is vital for diversified risk management.
We’ll discuss this more in the strategic allocation approach below.
The Psychology of Position Sizing
The size of a position can impact a trader’s emotional response to market movements.
Oversized positions may lead to panic selling or greed-driven decisions, while undersized positions might result in regret and missed opportunities.
There’s a balance to it.
Position Sizing in Both Strategic & Tactical Allocation Approaches
Position sizing is important in both strategic and tactical asset allocation approaches.
The approach is in design position sizing strategies to manage risk, optimize returns, and align with an investor’s financial goals and risk tolerance.
Understanding how position sizing functions within these frameworks highlights its importance in achieving a balanced and resilient portfolio.
Strategic Asset Allocation and Position Sizing
Strategic asset allocation involves setting long-term investment targets and allocating assets accordingly, often based on historical returns, volatility, and correlations.
Strategies like the balanced beta or all-weather approach aim to construct portfolios that can withstand various market conditions by diversifying across asset classes with different environmental biases.
Position Sizing in Strategic Allocation
In this context, position sizing is about determining the proportion of the portfolio allocated to each asset class (e.g., stocks, bonds, commodities, alternatives) to achieve desired exposure levels.
For instance, in an all-weather portfolio, the position size for each asset class is calculated to balance the portfolio across different economic environments, considering factors like inflation, growth, discount rates, risk premiums, and changes in their discounted expectations.
The goal is to minimize volatility and drawdowns for a given level of return while capturing upside potential across various scenarios.
Tactical Asset Allocation and Position Sizing
Tactical asset allocation, on the other hand, allows for short-term deviations from the strategic asset mix to capitalize on perceived market inefficiencies, economic trends, or informational, analytical, and/or technological advantages.
It involves actively adjusting position sizes within asset classes or sectors based on short-term forecasts and market conditions.
Position Sizing in Tactical Allocation
Here, position sizing becomes a dynamic way to manage risk and enhance returns.
For example, if short-term analysis suggests an upcoming bull market in technology stocks, a tactically managed portfolio might increase the position size in this sector temporarily.
Similarly, if fixed-income markets are expected to underperform due to rising interest rates, the position size in bonds might be reduced.
Or if an economy is late cycle, a trader might tilt the portfolio toward consumer staples (products with more stable demand) over consumer discretionary (products with more cyclical demand).
Tactical asset allocation requires more frequent adjustments to position sizes to reflect changing market conditions and outlooks.
Integrating Position Sizing with Asset Allocation Strategies
Risk Management
Both strategic and tactical allocation strategies use position sizing as a fundamental risk management tool.
In strategic asset management, position sizing is more about achieving balance and spreading things out in an efficient way.
By carefully sizing positions according to the portfolio’s long-term strategy and short-term adjustments, traders can manage exposure to market volatility, valuation, and other considerations.
Adaptability
Strategic allocation sets a baseline for exposure, while tactical adjustments enable the portfolio to pivot as needed, and better optimize for current market conditions.
Performance Optimization
Proper position sizing can help optimize the portfolio’s performance by making sure that capital is allocated efficiently, and is balanced between growth and risk mitigation.
Diversification
In the context of asset allocation, position sizing contributes to diversification not just within asset classes but also across them, as well as geographic and currency risk considerations.
Conclusion
Understanding and applying the principles of position sizing is fundamental for both novice and experienced traders.
It integrates risk management with trading strategy, and helps traders achieve optimal performance and emotional stability within the markets.