19+ Greeks to Know for Options Pricing [First-, Second-, and Third-Order Greeks]

In quantitative finance and especially with respect to options pricing, Greek letters are used to relate the sensitivity of the option price to changes in the underlying parameters, such as:

• price (delta)
• rate of change of price (gamma)
• time (theta)
• volatility (vega), and
• interest rate (rho)

They are often simply referred to as ‘the Greeks’ in finance, trading, and investing circles.

They are also commonly labeled hedge parameters or risk measures.

The Greeks are relevant to all types of options pricing, no matter the underlying asset (e.g., stocks, bonds, currencies, commodities).

Greeks for Options Pricing

Below are the five that are most relevant to options pricing:

Delta

Delta indicates how much you will make or earn should the underlying asset increase by $1.

If delta is equal to 0.524, that means for every one-dollar increase in the underlying asset, you will make $0.524 per share. Per options contract, which has 100 shares, you would make $52.40.

It’s important to note that:

• Call options always have positive deltas.
• Put options have negative deltas.

Deep in-the-money (ITM) options will have deltas near 1, where profit is almost tick-for-tick with the price of the underlying.

Deep out-of-the money (OTM) options will have deltas near 0 and move minimally with the price of the underlying.

Theta

Theta measures the time decay of an option.

For options that are at-the-money, theta will increase as the options approaches expiration.

For in-the-money or out-of-the-money options, theta will decrease the closer to expiration.

Theta helps to explain how time will erode (or increase) the value of an option.

The further out in time before expiration, theta will not decay as fast as it will closer to settlement.

Longer-term options are therefore better for strategies that depend less on the ability of time decay to diminish an option’s value.

A shorter-term option will be better for special option strategies that seek to profit from time decay.

Vega

Vega measures the sensitivity of the price of the option to volatility.

Vega has a tendency to be thought of as precisely synonymous with volatility, due to the fact that they both start with the letter V.

However, volatility is described through sigma, while vega is a property of the actual option itself rather than an input parameter like volatility.

An increase in volatility will naturally increase the price of both call and put options.

Likewise, a decrease in volatility will decrease the price of both call and put options. However, each option is a bit different regarding the sensitivity of its price change due to volatility, which is quantified through vega.

Higher vegas are seen for at-the-money options, while lower vegas are seen for in-the-money or out-of-the-money options.

Vega does not have a 50-50 distribution on each side of the underlying price. It does not decrease as readily as the underlying price increases.

This is due to the how underlying price works within the mathematical definition of vega, keeping vega higher at the top-end of the distribution.

For instance, for a stock with a strike price of 100, vega will be higher at a price of 105 than it will be for 95, despite each being the same distance from the strike price.

Rho

Rho is the rate at which the price of an option changes relative to the risk-free interest rate.

Hence every time an interest rate changes (which can relate to any maturity along the yield curve), it will affect the value of rho.

If an option has a rho value of 5.17, for every one-percent increase in interest rate, the option will obtain an additional value of 5.17%.

For call options, the value of rho will be positive. For put options, the value of rho will be negative.

Lambda

Lambda,, omega,, or elasticity is the percentage change in an option value’s per percentage change in the underlying price.

Lamba is considered a measure of leverage, which is sometimes referred to as gearing.

Epsilon

Epsilon, (also known as psi,), is the percentage change in the option value per percentage change in the underlying dividend yield.

This is considered a measure of the dividend risk. In the financial world, the dividend yield impact is determined using a 10 percent increase in those yields.

This sensitivity can only be applied to derivative instruments of equity products.

Second-order Greeks

Second-order Greeks are higher-order Greeks that take into account the changes in the underlying Greeks.

The most popular second-order Greeks are gamma, vanna, and charm.

These higher-order Greeks give a trader a more complete understanding of how their position will react to the underlying or other Greeks.

These Greeks can be useful in managing a portfolio of options and other derivatives.

Gamma

Gamma denotes the rate of change of delta as the price of the underlying changes.

It is essentially the derivative of delta with respect to price of the underlying.

Gamma is highest for options that are at-the-money (ATM).

They will change minimally for very deep in-the-money or deep out-of-the-money options.

Gamma vs. Delta

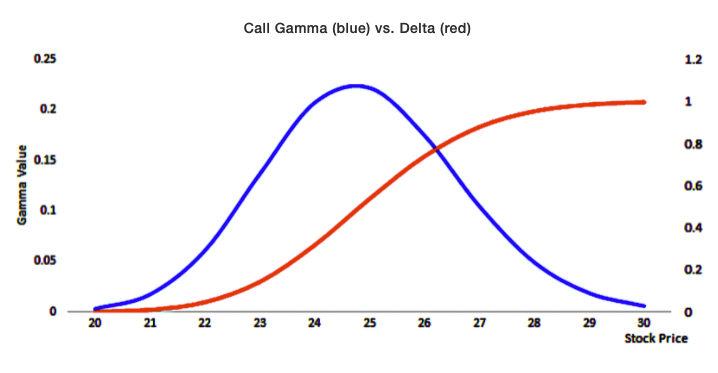
Gamma is also often described as the rate of change of an option’s delta per 1-point (or percentage point) move in the underlying asset’s price.

Gamma is the second derivative of the value function with respect to the underlying price.

Most long options will have positive gamma and most short options will have negative gamma.

Long options have a positive relationship with gamma. This is because as price increases, Gamma will increase as well, which causes Delta to approach 1 from 0 (long call option) and 0 from −1 (long put option). The inverse of this is true for short options.

Gamma is greatest approximately at-the-money (ATM) and falls the more out you go in-the-money (ITM) or out-of-the-money (OTM).

When traders try to delta hedge a position, they might also try to neutralize the portfolio’s gamma.

This helps ensure that the hedge will be effective not just under a small range of price movements (like in the case of delta hedging) but over a broader range and help correct for the convexity of value.

Vanna

Vanna is the rate of change of an option’s vega per 1-point (or percentage point) move in the underlying asset’s price.

Vanna is also known as:

• DvegaDspot and
• DdeltaDvol

It is a second order derivative of the option’s value, once to the underlying spot price and once to volatility.

It is the equivalent of DdeltaDvol, which is the sensitivity of the option delta with respect to change in volatility.

Because Vanna tracks delta and vega, it can be useful to monitor when maintaining a delta- and/or vega-hedged portfolio.

Vanna can help the trader to anticipate changes to the effectiveness of a delta-hedge as volatility changes or the effectiveness of a vega-hedge due to changes in the underlying asset.

Charm

Charm is the rate of change of an option’s delta per 1-point (or percentage point) move in time to expiration.

Charm is also called DdeltaDtime. Charm can be an important Greek for traders to look at when delta hedging a position over periods where markets close, such as a weekend or extended holiday.

Charm is a second-order derivative of the option’s value, once to delta (price) and once to theta (the passage of time). It’s also accordingly the derivative of theta with respect to the underlying asset’s price.

The mathematical result of the formula for charm is expressed in delta/year.

It can be informative to divide this by the number of days until an option’s expiration to arrive at the delta decay per day.

This use is relatively accurate when the number of days remaining until option expiration is large. However, when an option is near expiration, charm may change quickly, making this estimation of delta decay inaccurate.

Vomma

Vomma is also known as:

• volga
• vega convexity, or
• DvegaDvol

It measures second order sensitivity (the convexity) of an option’s value to volatility. In other words, vomma measures the rate of change to vega as volatility changes.

Under positive vomma, a position will become long vega as implied volatility goes up and short vega as it does down. Vomma can be scalped by traders in a way much like being long gamma.

So, some traders trying to scalp vomma will try to design a vega-neutral, long-vomma position, which can be constructed from ratios of options at different strike prices. It’s a strategy that’s difficult for an individual trader to pull off, given the need for software to keep track of exposures and the need to get in and out quickly.

Vomma is positive for long options that are out of the money, and initially increases with distance from the money (but it drops off as vega drops off).

Veta

Veta, which is also known as DvegaDtime, measures the rate of change in vega with respect to the passage of time.

Veta is the second derivative of the value function, once to volatility and once to time.

Vera (rhova)

Vera, also known somewhat less commonly as rhova, measures the rate of change in rho with respect to volatility.

Vera is the second derivative of the value function; once to volatility and once to interest rate.

Vera is generally the least popular of the second order Greeks as measuring changes in rho as it pertain to changes in volatility are not as common. Vera hedging is nowhere near as popular as gamma hedging.

The term ‘Vera’ was coined in 2012 when this sensitivity was to be used to assess the impact of volatility changes on rho-hedging, but it lacked a popular name, outside something more descriptive, like DrhoDvol.

‘Vera’ was chosen as something of a mashup to Vega and Rho, its respective first-order Greeks. Rhova is another variation of that, but Vera is more popular, as it’s also similar to Vega and Veta.

Third order Greeks

Third order Greeks continue off their first and second order counterparts.

The most important four are:

• Speed
• Zomma
• Color
• Ultima

Speed

Speed is also known as DgammaDspot or “the gamma of the gamma”.

Speed is the third derivative of the value function with respect to the underlying spot price.

It’s the third derivative in the chain after delta and gamma. So speed can be important to monitor when delta hedging or gamma hedging an exposure or an overall portfolio.

Speed is a relatively unpopular Greek because it is more difficult to trade than the others, but it’s generally true for all third order Greeks, as they start to become more complex.

You rarely hear of a “speed hedge” and often hedges can shift risk into other forms, such as creating unwanted vega or delta exposures.

Zomma

Zomma is sometimes called DgammaDvol.

Zomma is the third derivative of the option’s value, twice to the underlying asset price and once to volatility.

If a trader is running a gamma hedged portfolio, zomma can help a trader monitor how effectively the hedge is performing as volatility changes.

Color

Color, also known gamma decay or DgammaDtime, measures the rate of change of gamma with respect to the passage of time.

Color is a third order derivative of the option’s value, twice to delta (or once to gamma) and once to time.

Color is sometimes used by traders who are gamma hedging a position or portfolio so they can monitor how well the hedge is doing as time passes.

Mathematically, color is expressed in gamma per year. So, traders may take the result and divide by 365 – i.e., the number of days per year – to find the amount of gamma per day.

If there are lots of days before expiry, this measure is relatively accurate. However, the closer to expiration, the more the deviation.

Ultima

Ultima, also known as DvommaDvol, measures the sensitivity of the option vomma with respect to change in volatility, or the change in vega convexity with respect to volatility.

Ultima is essentially the third order derivative of the option’s value to volatility.

Multi-Asset Options Greeks

If the value of a derivative is dependent on two or more underlyings, its Greeks are extended to include the cross-effects between the underlyings.

Correlation delta

Correlation delta, also known as cega, measures the change in the value of a derivative when the correlation between two underlyings changes.

Correlation gamma or cross gamma

Correlation gamma measures how the delta of an option changes when the correlation between two underlyings changes.

It is used in multi-asset options to help manage a delta-hedged portfolio when correlations change.

Correlation vanna or cross vanna

Correlation vanna, also known as cvanna, measures how the vega of an option changes when the price of the underlying asset changes in the other.

In other words, it measures how delta changes in the second underlying due to a change in the volatility of the first underlying.

It is used in multi-asset options to help manage a vega-hedged portfolio when correlations change.

Correlation veta or cross veta

Correlation volga measures the rate of change of vega in one underlying asset to a change in the volatility of another underlying asset.

Practical application of correlation Greeks or cross Greeks

These Greeks are sometimes referred to as “cross Greeks” because they measure how one underlying affects another. For example, if asset A has a positive correlation with asset B, then an increase in the price of A will likely lead to an increase in the price of B. In this case, the correlation gamma of A would be positive.

These Greeks can be used to manage multi-asset portfolios when correlations change.

For example, if a portfolio is delta and vega hedged, and the correlation between the two underlying assets change, the hedges may no longer be effective. In this case, the trader can use the cross Greeks to adjust the hedges.

What Are ‘Flows’ with Respect to Option Greeks?

Greek flows are a metric followed by options market makers (and potentially other types of traders).

When someone mentions Greek “flows,” they’re describing the impact of these Greeks on market dynamics due to trading activity and hedging adjustments.

The table provided earlier in the article, and again below, categorizes various Greeks and higher-order Greeks according to their sensitivities with respect to:

• spot price (S)
• volatility (σ), and
• the passage of time (t)

Below is a description of flows associated with each of these Greeks (we’ll define each term again so the flows explanation makes better sense):

Spot Price (S) Related Flows

Delta (Δ)

• Definition – Sensitivity of the option’s price to changes in the underlying asset’s price.
• Flows – When Delta changes due to movements in the underlying asset’s price, market makers adjust their hedges by buying or selling the underlying asset to maintain a neutral position (delta hedging).

Gamma (Γ)

• Definition – Measures Delta’s rate of change with respect to changes in the underlying asset’s price.
• Flows – Gamma hedging involves frequent adjustments to the Delta hedge. Large Gamma exposures can lead to increased trading volumes in the underlying asset as market makers adjust their positions more aggressively. Gamma squeeze is sometimes talked about.

Speed

• Definition – The rate of change of Gamma with respect to changes in the underlying asset’s price.
• Flows – Speed impacts how quickly Gamma changes, influencing the frequency and size of hedging adjustments by market makers.

Volatility (σ) Related Flows

Vega (ν)

• Definition – Measures the sensitivity of the option’s price to changes in the volatility of the underlying asset.
• Flows – Significant changes in implied volatility lead to adjustments in Vega. This prompts market makers to trade options or other volatility-sensitive instruments to manage their risk.

Vanna

• Definition – Measures the sensitivity of Delta to changes in volatility.
• Flows – When volatility changes, Vanna affects Delta, leading to hedging adjustments. This can cause additional buying or selling of the underlying asset to maintain a Delta-neutral position.

Vomma

• Definition – The sensitivity of Vega to changes in volatility.
• Flows – Changes in volatility lead to adjustments in Vomma. Impacts Vega and requiring further hedging activities involving volatility instruments.

Zomma

• Definition – Measures the sensitivity of Gamma to changes in volatility.
• Flows – Variations in volatility affect Gamma through Zomma. Leads to changes in the frequency and intensity of Delta hedging.

Ultima

• Definition – Measures the sensitivity of Vomma to changes in volatility.
• Flows – Significant volatility shifts impact Vomma through Ultima, influencing Vega and resulting in complex hedging strategies involving multiple Greeks.

Passage of Time (t) Related Flows

Theta (θ)

• Definition – Measures the sensitivity of the option’s price to the passage of time.
• Flows – As options approach expiration, Theta causes the option’s price to decay. This time decay requires market makers to adjust their hedges continuously. Affects their positions in the underlying asset.

Charm

• Definition – The sensitivity of Delta to the passage of time.
• Flows – As time progresses, Delta changes due to Charm, leading to adjustments in the hedging of the underlying asset to maintain a Delta-neutral position.

Veta

• Definition – The sensitivity of Vega to the passage of time.
• Flows – As time passes, changes in Vega due to Veta necessitate adjustments in volatility hedges, impacting the trading of options and other volatility-related instruments.

Color

• Definition – Measures the rate of change of Gamma over time.
• Flows – The impact of time on Gamma through Color requires ongoing adjustments to the Delta hedging strategy, influencing trading volumes in the underlying asset.

The associated flows describe the necessary hedging activities by market makers to maintain neutral positions in response to changes in these parameters.

These hedging activities, in turn, influence the trading dynamics of the underlying assets and derivatives.

Related

• Options Pricing Models: 11 Ways to Value Options and Derivatives