Copulas in Trading, Investing, Portfolio Management, and Risk Management

Copulas have become a valuable tool in the field of quantitative finance, particularly in the areas of trading, investing, portfolio management, and risk management.

They are widely used to model and minimize tail risk, as well as in portfolio optimization applications.

This article explores the various ways in which copulas are utilized in financial markets and highlights typical finance applications.

Key Takeaways – Copulas in Trading, Investing, Portfolio Management, and Risk Management

• Copulas are a tool in quantitative finance for modeling the dependence between different assets and financial instruments, enabling better risk management and optimal strategies.
• They are widely used to analyze systemic risk, price complex options, optimize portfolios, and forecast returns, leading to more accurate measurements and improved decision-making.
• Copulas have limitations and require careful consideration of the appropriate function and parameters.
• But when used in conjunction with other risk management tools, they offer insights into financial risks and opportunities.

Copulas – A Brief Overview

Copulas are mathematical functions that describe the dependence between random variables.

In the context of finance, they are used to model the joint behavior of different assets or financial instruments, allowing investors and risk managers to gain insights into the relationships between these assets and devise optimal strategies for managing risk and maximizing returns.

Typical Finance Applications

Analyzing Systemic Risk in Financial Markets

Copulas can be employed to measure and analyze systemic risk in financial markets by modeling the dependence between different assets and financial institutions.

This helps regulators and market participants to better understand the potential consequences of market shocks and develop appropriate risk mitigation strategies.

Pricing Spread Options and Fixed Income Constant Maturity Swap Spread Options

Copulas are used to analyze and price spread options, particularly in the context of fixed income constant maturity swap spread options.

By modeling the joint behavior of the underlying assets, copulas help derive more accurate option prices and identify potential arbitrage opportunities.

Analyzing and Pricing Volatility Smile/Skew of Exotic Baskets

In the pricing of exotic basket options, such as knock-ins or knock-outs, best-of/worst-of, etc., copulas play a role in modeling the volatility skew of the underlying assets.

This allows for more accurate pricing of these financial instruments.

Pricing Volatility Smile/Skew of Less Liquid FX Crosses

In less liquid foreign exchange (FX) markets, copulas are employed to model the volatility smile/skew of the currency pairs involved.

This enables more accurate pricing of options on these currency pairs, as well as better risk management for trading strategies.

Value-at-Risk Forecasting and Portfolio Optimization

Copulas are used in value-at-risk (VaR) forecasting and portfolio optimization to minimize tail risk for equities and other markets.

By modeling the dependence between assets, copulas provide a more accurate measure of portfolio risk and help investors create more efficient portfolios.

Forecasting Equities Returns for Higher-Moment Portfolio Optimization

By capturing the dependence structure between equities, copulas can be used to forecast returns for higher-moment portfolio optimization, leading to better investment decisions and improved portfolio performance.

Improving Estimates for Sophisticated Mean-Variance Optimization Strategies

Copulas can help improve the estimates of a portfolio’s expected return and variance-covariance matrix, which are important inputs for more sophisticated mean-variance optimization strategies.

This results in more efficient portfolio construction and better risk-adjusted performance.

Statistical Arbitrage Strategies, Including Pairs Trading

In statistical arbitrage strategies, such as pairs trading, copulas are used to model the dependence between assets, allowing traders to identify and exploit temporary price inefficiencies in the market.

How to Create a Copula Test for Financial Forecasting

You can run a copula test using any standard statistical software.

In R, here is an example model using Value-at-Risk (VaR) forecasting for a portfolio with 10% annualized returns and 20% volatility whose returns are normally distributed.

Steps to Creating a Copula Test (Example)

1. Install and load the necessary packages (specifically designed for R):

install.packages("copula") 
install.packages("ggplot2") 
library(copula) 
library(ggplot2)

2. Define the portfolio characteristics:

returns <- 0.10 # Annualized returns 
volatility <- 0.20 # Volatility

3. Generate random returns based on a normal distribution:

set.seed(123) # Set a seed for reproducibility
n_samples <- 1000 # Number of samples to generate
portfolio_returns <- rnorm(n_samples, mean = returns, sd = volatility)

4. Create a Gaussian copula object:

copula_model <- normalCopula(param = 0)

5. Generate correlated random variables using the copula:

correlated_returns <- rCopula(n_samples, copula_model)

6. Transform the correlated returns into the desired distribution (e.g., normal distribution):

correlated_returns <- qnorm(correlated_returns, mean = returns, sd = volatility)

7. Calculate the VaR at a given confidence level (e.g., 95%):

confidence_level <- 0.95
VaR <- quantile(correlated_returns, 1 - confidence_level)

8. Plot the histogram of portfolio returns and mark the VaR level:

df <- data.frame(portfolio_returns)
ggplot(df, aes(x = portfolio_returns)) +
geom_histogram(binwidth = 0.02, color = "black", fill = "lightblue") +
geom_vline(xintercept = VaR, color = "red", linetype = "dashed", size = 1) +
labs(title = "Portfolio Returns Histogram",
x = "Portfolio Returns",
y = "Frequency") +
theme_minimal()

Running the above code will generate a histogram plot with the VaR level marked.

In this case, this diagram says for this particular portfolio its 95% VaR is about -23% (95% likelihood that it will not lose more than 23% within one year).

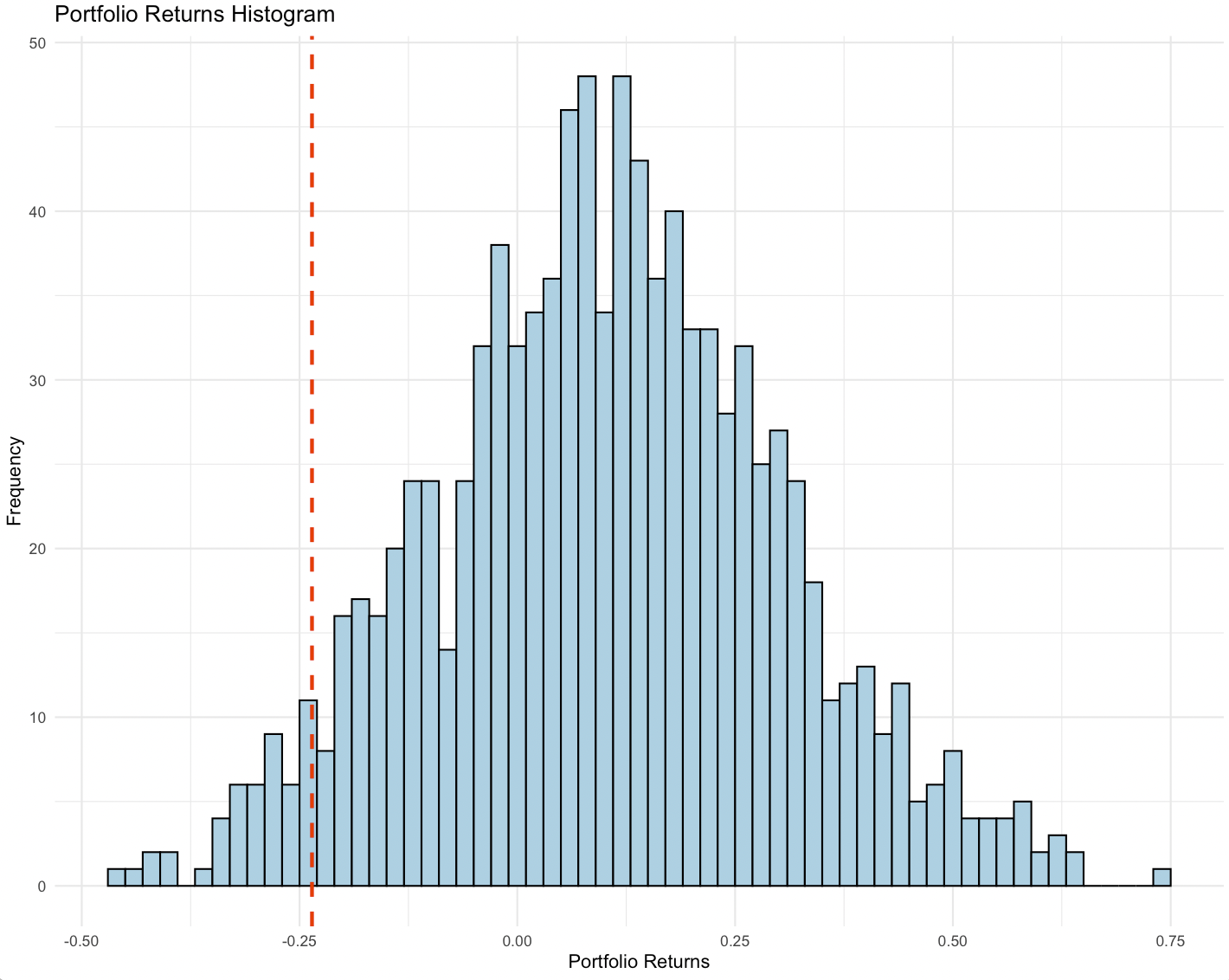
Please note that using copulas requires specifying the correlation structure between the assets in the portfolio. In this case, we already know the mean and variance of the overall portfolio.

You may need to modify the code to fit your specific copula model if you have additional assets with different correlations.

FAQs – Copula in Trading, Investing, Portfolio Management, and Risk Management

What is a copula and why is it important in finance?

A copula is a mathematical function that describes the dependence between random variables.

In finance, copulas are essential for modeling the joint behavior of different assets or financial instruments.

They provide insights into the relationships between these assets, enabling investors and risk managers to make more informed decisions and devise optimal strategies for managing risk and maximizing returns.

How do copulas differ from other correlation and covariance analysis techniques?

Copulas are mathematical functions used in statistics to model and analyze the dependence structure among multiple variables, going beyond traditional correlation and covariance measures.

Correlation and covariance are limited as they only capture linear relationships and measure the degree of dependence between two variables.

However, copulas allow for the modeling of more intricate interdependencies, including both linear and non-linear relationships, and are not restricted to just two variables.

They can provide a much richer understanding of the structure of multivariate data.

Importantly, copulas separate marginal distributions of individual variables from their dependence structure, making them particularly useful in fields like finance and insurance, where understanding and modeling the dependencies between variables is important.

How are copulas used to analyze systemic risk in financial markets?

Copulas can be employed to measure and analyze systemic risk in financial markets by modeling the dependence between different assets and financial institutions.

By understanding these relationships, regulators and market participants can better anticipate the potential consequences of market shocks and develop appropriate risk mitigation strategies.

Can copulas be applied to all types of financial assets and instruments?

Copulas can be applied to a wide range of financial assets and instruments, including equities, fixed income securities, currencies, and derivatives such as options and swaps.

However, the choice of copula and its parameters should be carefully considered to accurately reflect the specific characteristics and dependencies of the assets being modeled.

How do copulas improve portfolio optimization?

By modeling the dependence between assets, copulas provide a more accurate measure of portfolio risk, helping investors create more efficient portfolios that maximize returns while minimizing risk.

Copulas can be used in value-at-risk forecasting, higher-moment portfolio optimization, and sophisticated mean-variance optimization strategies to improve portfolio construction and risk-adjusted performance.

What is the role of copulas in pricing exotic options and less liquid FX crosses?

In the pricing of exotic options, such as best/worst-of options, and less liquid FX crosses (e.g., EM FX), copulas play an important role in modeling the volatility smile or skew of the underlying.

By capturing the joint behavior of these assets, copulas allow for more accurate pricing of these complex financial instruments, as well as better risk management for trading strategies.

Are there any limitations to using copulas in finance?

While copulas are a tool for modeling dependencies between financial assets, they do have some limitations.

One key challenge is selecting the appropriate copula function and its parameters to accurately reflect the dependence structure of the assets being modeled.

Moreover, copulas may not fully capture extreme events or tail risks, and they rely on historical data, which may not always be a reliable predictor of future market behavior.

Can copulas be used in conjunction with other risk management tools?

Yes, copulas can be used in combination with other risk management tools and techniques, such as stress testing, scenario analysis, and sensitivity analysis.

By incorporating copulas into these approaches, traders/investors and risk managers can gain a more comprehensive understanding of the potential risks and opportunities in their portfolios and make better-informed decisions.

Conclusion

Copulas have become a valuable tool in quantitative finance, offering insights into the relationships between assets and their risks.

By leveraging copulas in various applications, such as analyzing systemic risk, pricing complex options, and optimizing portfolios, investors and risk managers can make more informed decisions and achieve better outcomes.