First-Hitting-Time Model – Applications in Trading

The First-Hitting-Time Model (FHTM) is a mathematical concept that originates from the field of stochastic processes, which we’ve covered in our article on probability theory in trading.
It’s more recently gained prominence in finance, particularly in trading and portfolio management.
The model is used to predict the time it takes for a random process to reach a pre-determined threshold, and it can be employed to analyze and forecast financial market dynamics.
In this article, we’ll look at the FHTM, focusing on its applications to trading and managing portfolios.
Key Takeaways – First-Hitting-Time Model
- The First-Hitting-Time Model (FHTM) is a mathematical tool used in finance to predict how long it will take for a random process to reach a specific level.
- FHTM helps traders manage risk by estimating the probability of an asset’s price reaching a certain level within a given time frame.
- In portfolio management, FHTM assists in optimizing asset allocation, assessing risk, and conducting scenario analysis to make informed investment decisions.
- We run a simulation using the FHTM as it applies to the “Gambler’s Ruin” problem.
Understanding the First-Hitting-Time Model
Definition of FHTM
The First-Hitting-Time Model is a statistical method that estimates the probability of a stochastic process reaching a certain level within a given time frame.
It considers the time it takes for the process to “hit” this level for the first time, providing insights into the behavior of the underlying process.
Stochastic Processes and FHTM
In finance, stochastic processes are widely used to model the seemingly random movements of asset prices, interest rates, and other financial variables.
FHTM is particularly applicable to financial markets, as it can be used to determine the likelihood of specific events occurring, such as market crashes, price spikes, or trends.
In Very Simple Terms, What Is the First-Hitting-Time Model?
To keep things simple, we can explain First-Hitting-Time Model as a tool that helps traders understand when something might happen in the future based on how things have happened in the past.
The FHTM is based on the idea that financial markets and other random processes can be represented by patterns that go up and down.
The patterns may appear somewhat random on a chart, but with trending moves in either direction for extended periods of time when zooming out, they look less random.
The model tries to figure out how long it might take for the asset to reach a certain price point.
Traders use the FHTM to help them manage risk. They can estimate the chance of a price going down to a certain level within a specific time. This helps them decide if they should buy or sell something, such as options or a less correlated asset.
The FHTM is also useful for developing trading strategies. Traders can use it to predict if prices will suddenly go up or down, so they can make smart decisions about when to buy or sell.
For those who manage a lot of money, like in a pension fund or an investment firm, the FHTM helps them decide how much to allocate into different assets. It can estimate the chance of each investment reaching a certain level of profit.
This information helps them make better decisions about how to invest, so they can make better returns while taking less risk.
Applications to Trading
Risk Management
One of the primary applications of FHTM in trading is risk management.
Traders can use FHTM to estimate the probability of an asset’s price reaching a pre-determined stop-loss level within a specified time period.
This helps them decide whether to enter or exit a position, allowing for better risk control.
Trading Strategies
FHTM can also be used to develop and enhance trading strategies.
For instance, traders can use the model to predict the likelihood of price breakouts or reversals, allowing them to position themselves accordingly.
Moreover, FHTM can be employed to fine-tune entry and exit points in various trading strategies, improving their overall performance.
Applications to Portfolio Management
Portfolio Optimization
In portfolio management, the FHTM can be used to optimize asset allocation by estimating the probability of each asset in the portfolio reaching a specific return threshold.
This information can help portfolio managers make more informed decisions about asset allocation, maximizing returns while minimizing risk.
We have more on portfolio optimization strategies here.
Risk Assessment
FHTM can also be applied to assess the overall risk of a portfolio.
By estimating the probability of the portfolio reaching a certain loss level, portfolio managers can better understand the risk they are exposed to and make adjustments accordingly.
This can lead to more robust and resilient portfolios.
Scenario Analysis
The FHTM can be employed in scenario analysis, allowing portfolio managers to evaluate the potential impact of different market events on their portfolios.
By simulating various market scenarios and examining the associated first-hitting times, managers can gain insights into how their portfolios might perform under different conditions, enabling them to make strategic adjustments when needed.
First-Hitting-Time Model in the Context of the “Ruin Problem”
The “ruin problem,” also known as the Gambler’s Ruin, is a classic problem in probability theory that deals with a gambler’s chances of going bankrupt (i.e., “ruin”) given a certain amount of initial wealth, betting strategy, and probability of winning each bet.
The First-Hitting-Time Model (FHTM) is particularly relevant in this context, as it can be used to determine the time it takes for the gambler to either reach a pre-determined wealth level or go bankrupt.
In the Gambler’s Ruin problem, the gambler’s wealth is represented as a random walk, which is a simple stochastic process.
The gambler starts with a certain amount of wealth and makes bets of fixed size.
With each bet, the gambler’s wealth either increases or decreases by the bet amount, depending on whether they win or lose.
The FHTM can be used to calculate the probability of the gambler reaching a specific wealth level or ruin within a given time frame, shedding light on the gambler’s likelihood of success or failure.
Example
Let’s say a gambler starts with:
- an initial balance of $1,000
- plays a game with a 50% chance of success each round
- has an initial bet size of $50
- doubles his bet size each time he loses (Martingale strategy)
- if he gets to $2,000 before he wipes out, the game is won (so two outcomes: $2,000 or $0)
What are the odds of long-term success using this strategy?
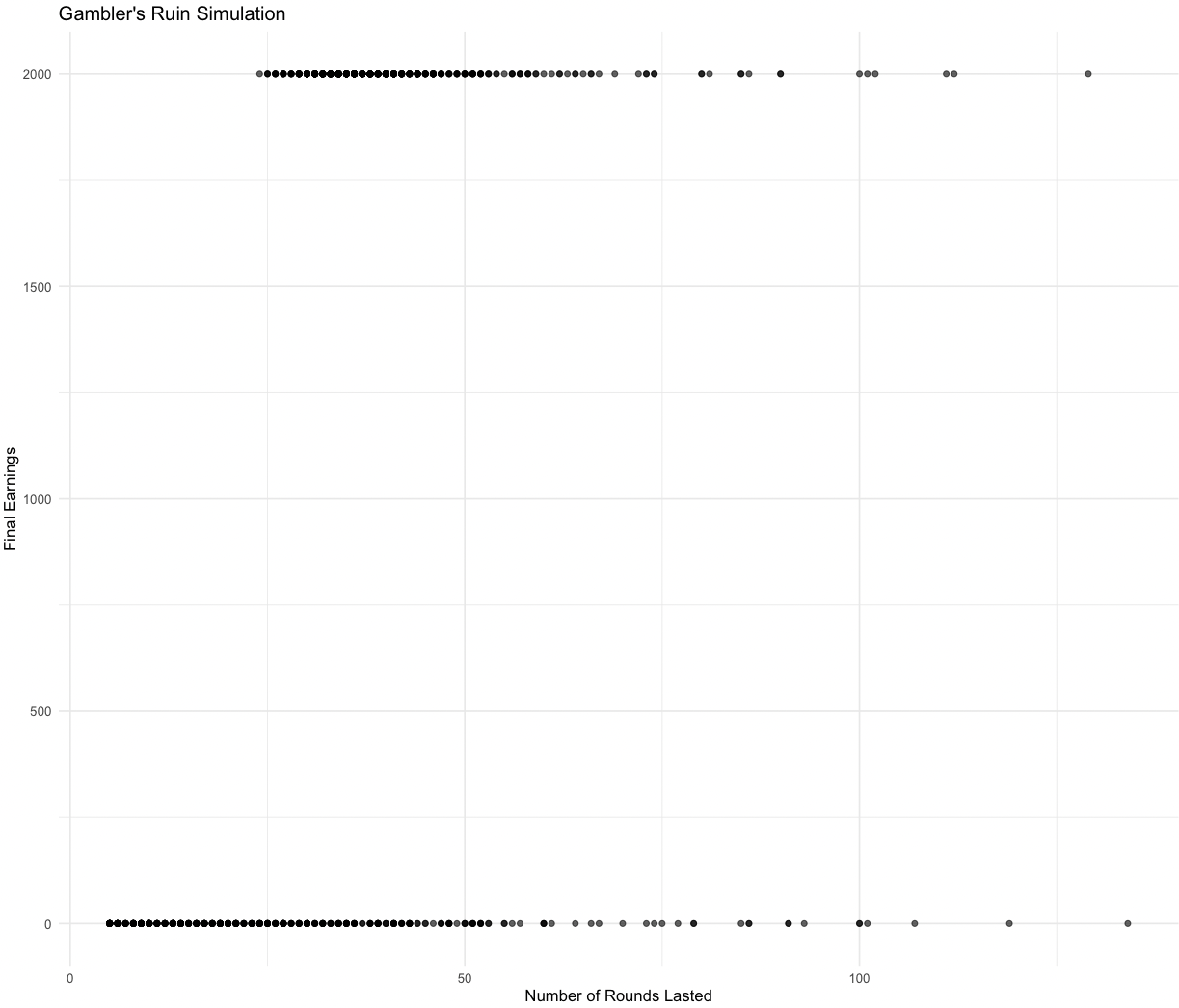
We ran 1,000 simulations.
We can see that failing early is more common than winning early. This is because of the Martingale strategy employed that multiplies the bet size.
We also see that failing is a bit more likely than winning.
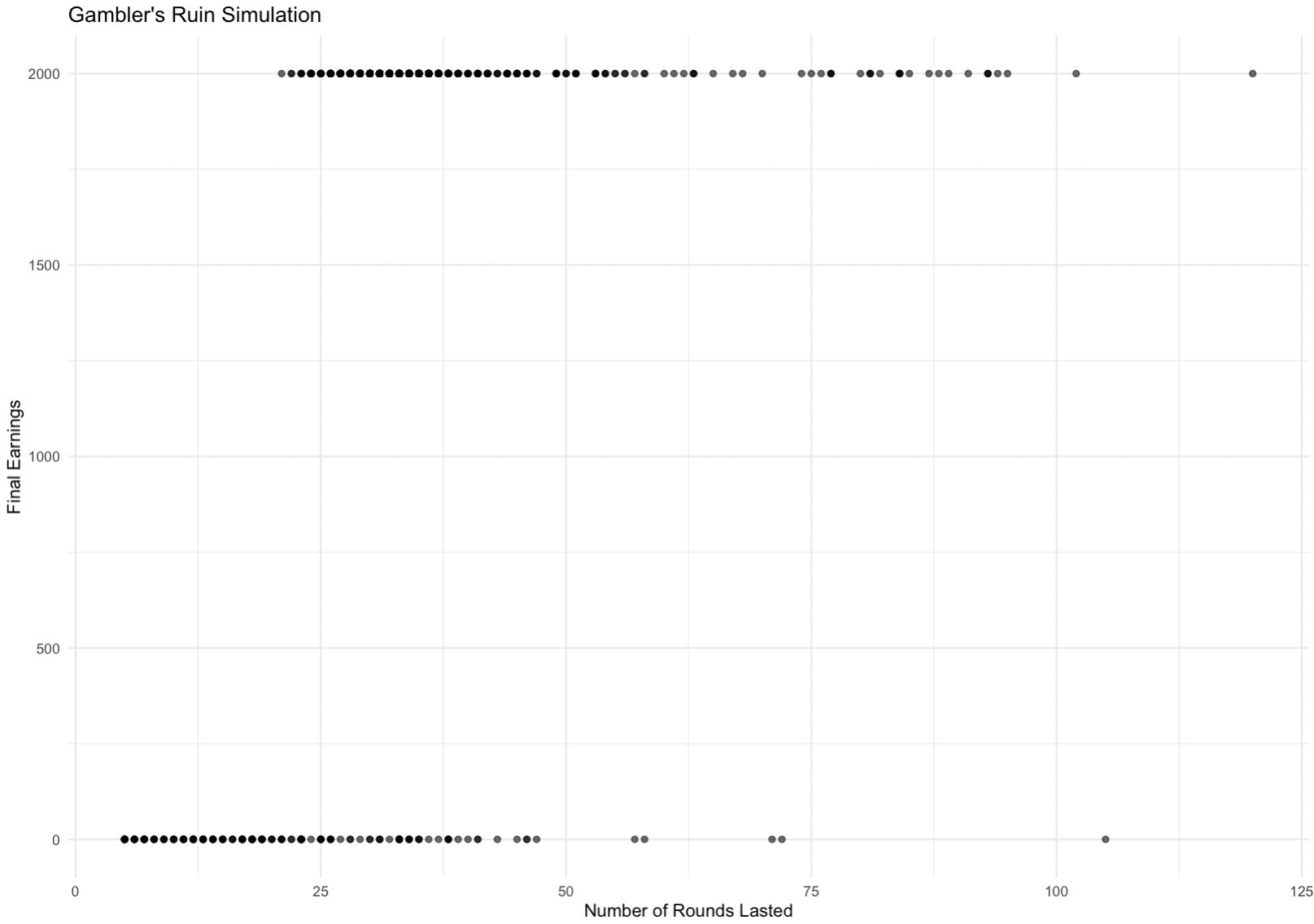
We can also simulate this with a win probability of 60% for each round, which naturally produces more wins (finishing with $2,000) than losses (finishing with $0), though failing early is still common due to the Martingale system employed.
First Passage Time Distribution for Brownian Motion
FAQ Section
What is the primary difference between the First-Hitting-Time Model and other models used in finance?
The primary difference between the First-Hitting-Time Model and other financial models lies in its focus on the time it takes for a stochastic process to reach a specified level, rather than the process’s final value or other characteristics.
This makes FHTM particularly relevant for analyzing events and risks associated with specific time frames.
How does the First-Hitting-Time Model help in managing risk in trading and portfolio management?
FHTM helps manage risk by estimating the probability of an asset’s price reaching a pre-determined level (e.g., a stop-loss level) within a specific time frame.
This information enables traders and portfolio managers to make better-informed decisions about entering or exiting positions, ultimately improving risk control.
Can the First-Hitting-Time Model be applied to other fields besides finance?
Yes, the First-Hitting-Time Model has applications in various fields, including physics, biology, and engineering.
In these areas, FHTM can be used to analyze the time it takes for a random process to reach a particular state or level, providing valuable insights into the behavior of the underlying process.
Is the First-Hitting-Time Model applicable to all types of financial markets and assets?
The FHTM is applicable to a wide range of financial markets and assets, including stocks, bonds, commodities, and currencies.
The model’s versatility comes from its ability to analyze stochastic processes, which are commonly used to represent the seemingly random movements of asset prices, interest rates, and other financial variables.
Can the First-Hitting-Time Model predict market crashes or extreme events?
While the FHTM can estimate the probability of a stochastic process reaching a certain level within a given time frame, it cannot predict specific events, such as tail risks (e.g., “market crashes”).
However, the model can provide insights into the likelihood of such events occurring within specific periods of time, which can help inform risk management and investment strategies.
How does the First-Hitting-Time Model relate to the Gambler’s Ruin problem?
The Gambler’s Ruin problem deals with the chances of a gambler going bankrupt, given a specific initial wealth, betting strategy, and probability of winning each bet.
The First-Hitting-Time Model can be used to determine the time it takes for the gambler to either reach a pre-determined wealth level or go bankrupt, making it relevant in the context of the ruin problem.
Conclusion
The First-Hitting-Time Model has proven to be a valuable tool in the realms of trading and portfolio management.
Its ability to estimate the probability of stochastic processes reaching specific levels within a given time frame makes it particularly relevant for risk management, strategy development, and portfolio optimization.
By leveraging the insights provided by the FHTM, traders and portfolio managers can make more informed decisions, enhancing the performance of their strategies and portfolios.