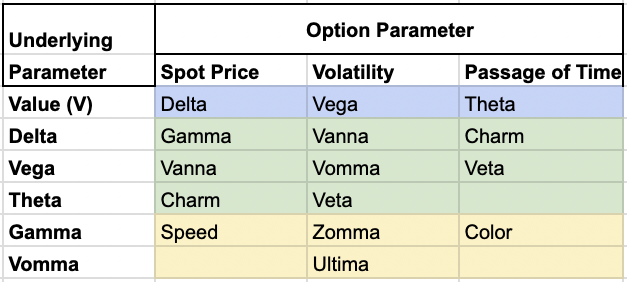
Vanna (Option Greek)

Vanna is a second-order Greek used in options trading and risk management. 

It measures: 

• the rate of change in an option’s vega with respect to changes in the underlying asset’s price, or
• the sensitivity of the option delta with respect to change in volatility

In other words, Vanna quantifies how an option’s sensitivity to volatility (vega) changes as the price of the underlying asset moves.

Accordingly, it’s also known as DdeltaDvol or DvegaDspot.

Key Takeaways – Vanna (Option Greek)

• Vanna measures how an option’s sensitivity to volatility changes with the underlying price
• Important for understanding complex price-volatility interactions in options.
• Positive for calls and negative for puts, Vanna is largest for at-the-money options.
  • Helps traders anticipate vega changes as prices move.
• Effective Vanna management can improve delta-hedging stability and improve volatility trading strategies, but requires frequent portfolio adjustments.
• Day traders could theoretically consider Vanna in their approach if they were particularly advanced, but it’s highly uncommon for individual traders to go beyond basic Greeks (e.g., theta, delta).
  • It is difficult for human traders, in general, to successfully trade multi-order Greeks.

Understanding Vanna

Definition

Vanna is mathematically expressed as the partial derivative of vega with respect to the underlying asset’s price, or alternatively, as the partial derivative of delta with respect to volatility:

Vanna = ∂Vega / ∂S = ∂Delta / ∂σ

Where:

• S is the price of the underlying asset
• σ (sigma) is the implied volatility

Significance in Options Trading

Vanna is useful in understanding the relationships between: 

• an option’s price
• the underlying asset’s price, and 
• volatility

It helps traders and risk managers assess how changes in these factors can affect their options positions.

Characteristics of Vanna

Sign and Magnitude

Vanna can be positive or negative:

• For call options, Vanna is typically positive
• For put options, Vanna is typically negative

The magnitude of Vanna is generally largest for at-the-money options and decreases for deep in-the-money or out-of-the-money options.

This is just like how Vega acts.

Relationship with Other Greeks

Vanna is closely related to other second-order Greeks:

• Charm (delta decay): Vanna = -Charm / σ
• Volga (vomma): Vanna = Volga / S

Applications of Vanna in Options Trading

Risk Management

Traders use Vanna to:

• Observe the stability of their delta-hedged positions
• Anticipate changes in their portfolio’s vega exposure as markets change

Trading Strategies

Vanna-aware strategies include:

• Volatility trading – Exploiting discrepancies between implied and realized volatility
• Delta-neutral vega trading – Constructing positions with specific vega exposure while minimizing delta risk

Calculating Vanna

Black-Scholes Model

In the Black-Scholes model, Vanna for a European option is given by:

Vanna = (d1 * d2) / (S * σ * √T) * e^(-q*T) * N'(d1)

Where:

• d1 and d2 are standard Black-Scholes parameters
• T is time to expiration
• q is the dividend yield
• N'(x) is the standard normal probability density function

Numerical Methods

Black-Scholes is a basic options pricing model.

For more complex options or in real-world scenarios, Vanna is often calculated using numerical methods such as:

• Finite difference approximations
• Monte Carlo simulations

Vanna Hedging

Vanna hedging is a strategy used to manage the risk associated with changes in an option’s vega as the underlying asset’s price moves.

It typically aims for a neutral Vanna position and is executed with algorithms.

It helps traders protect against simultaneous changes in the underlying price and volatility, which can impact option values.

Vanna hedging is most useful for complex options/volatility strategies or large portfolios where the interaction between price and volatility sensitivity is important.

It’s often used in conjunction with other Greeks hedging techniques to create a more thorough risk management approach.

Nonetheless, Vanna hedging can be challenging to implement due to its complexity and the need for frequent adjustments.

Hedging one thing can also shift the risk to other factors/variables.

How to Execute a Vanna Hedge

To execute a Vanna hedge:

1. Calculate your portfolio’s current Vanna exposure (requires software).
2. Determine your target Vanna (often zero for a neutral position).
3. Identify options with opposite Vanna to your current exposure.
4. Buy or sell these options to offset your Vanna.
5. Monitor and adjust your position as appropriate.
6. Use options with different strikes and expirations to fine-tune the hedge.
7. Consider transaction costs and liquidity when selecting hedge instruments. Algorithms are vastly more effective at executing these types of complex hedges relative to humans.

Regular rebalancing is important for maintaining an effective Vanna hedge.

Who Uses Vanna?

Vanna is primarily used by sophisticated market participants such as:

1. Market makers
2. Options trading desks at investment banks
3. Hedge funds specializing in volatility trading
4. Proprietary trading firms
5. Advanced individual options traders

These entities use Vanna to: 

• fine-tune their risk exposures
• optimize more advanced trading strategies, and 
• take advantage of subtle market inefficiencies in options pricing

Vanna Limitations & Considerations

Model Assumptions

Vanna calculations often rely on models with simplifying assumptions, which may not fully capture real-world market dynamics.

The Market Environment

The behavior of Vanna can change dramatically under extreme market conditions or during periods of high volatility.

Conclusion

Vanna helps options traders and risk managers understand the relationship between price, volatility, and option values.

Ultimately, the goal is help with decision-making and risk management.

But like all mathematical models in finance, it should be used in conjunction with other forms of analysis.