Bayesian Efficiency in Financial Markets

Bayesian Efficiency, based in Bayesian probability theory, is used in financial modeling and decision-making.

It involves updating the probability of a hypothesis as more evidence or information becomes available.

In finance, this concept is applied to continuously refine trading strategies and risk assessments based on incoming data.

Key Takeaways – Bayesian Efficiency

• Bayesian Efficiency applies Bayesian inference to financial markets.
• Involves constantly updating beliefs and predictions based on new information.
• It enhances market predictions and risk assessment by incorporating prior knowledge and real-time data.
• Bayesian Efficiency helps adapt to market changes with probabilistic approaches.
• We look at an example algorithm of how this might work.

Applications of Bayesian Efficiency in Financial Markets

Adaptive Portfolio Management

Bayesian Efficiency is used in adaptive portfolio management.

As new market data emerges, traders can update their beliefs about the market’s state and adjust their portfolios accordingly.

An example would be traders buying or selling a stock in response to an earnings release. (We’ll do an example algorithm of how this might work in this context below.)

This dynamic approach contrasts with static models and allows for more responsive trading or investment strategies.

Risk Assessment and Mitigation

In risk management, Bayesian methods enable traders to update and refine their risk assessments continually.

By integrating new information, such as economic indicators or company performance data, traders can recalibrate their risk models to better reflect current realities.

Strategic Implications for Traders/Investors

Data-Driven Decision Making

Bayesian Efficiency advocates for a data-driven approach to trading decisions.

It involves using probabilistic models to assimilate new information.

This helps enhance the accuracy of predictions about asset prices, market trends, and potential risks.

Enhanced Predictive Models

Incorporating Bayesian methods can lead to better predictive models.

These models are capable of adapting to new information, which makes them valuable in volatile or rapidly changing markets.

Importance of Prior Knowledge

Bayesian Efficiency underscores the importance of prior knowledge or beliefs in decision-making.

Initial assumptions or beliefs are updated as new data becomes available.

The idea is that we don’t throw out what we already knew, but rather update existing beliefs or assumptions.

Challenges & Considerations

Complexity of Implementation

Implementing Bayesian methods in finance is complex.

It requires advanced statistical knowledge and computational resources.

Investors must be proficient in probabilistic modeling and have access to reliable and timely data.

Handling of Subjective Priors

One challenge is the subjective nature of prior beliefs in Bayesian analysis.

Traders must carefully consider their initial assumptions, as these can significantly influence the outcomes of the Bayesian models.

Necessity for Continuous Data Integration

Bayesian Efficiency requires continuous integration of new data.

Traders need systems and processes in place to efficiently incorporate new information into their models and decision-making processes.

Coding Example – Bayesian Efficiency

Let’s create a Python coding example that exemplifies Bayesian Efficiency in financial markets.

We’ll do it with respect to updating stock price predictions after an earnings release.

We can use a simplified Discounted Cash Flow (DCF) model.

Bayesian Efficiency will be demonstrated by updating our prior beliefs about a company’s future cash flows based on the new information from the earnings release.

Here’s a conceptual Python script for this scenario:

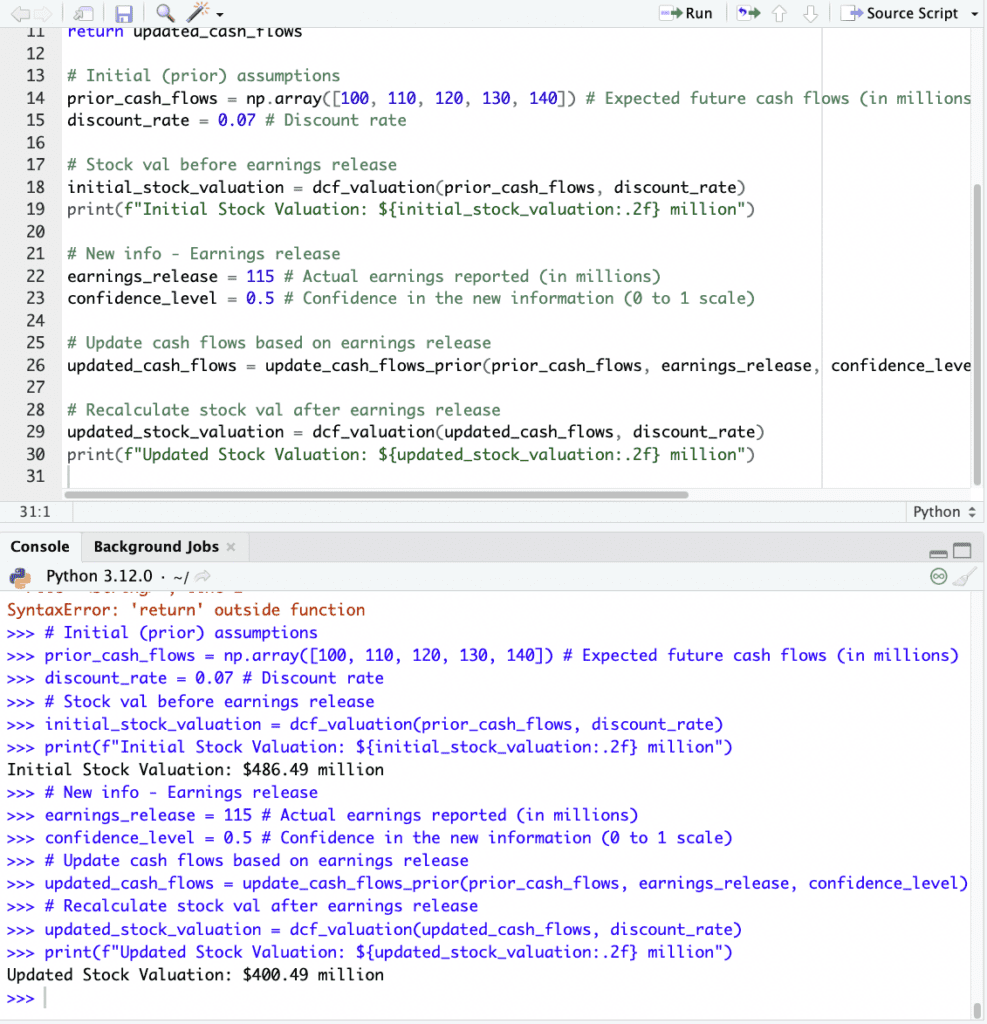
import numpy as np

def dcf_valuation(cash_flows, discount_rate):
""" Calculate the present value of future cash flows using DCF model. """
present_value = sum(cf / (1 + discount_rate) ** i for i, cf in enumerate(cash_flows, 1))
return present_value

def update_cash_flows_prior(prior_cash_flows, earnings_release, confidence_level):
""" Update prior cash flows based on earnings release using Bayesian approach. """
updated_cash_flows = prior_cash_flows * (1 + confidence_level * (earnings_release - np.mean(prior_cash_flows)) / np.std(prior_cash_flows))
return updated_cash_flows

# Initial (prior) assumptions
prior_cash_flows = np.array([100, 110, 120, 130, 140]) # Expected future cash flows (in millions)
discount_rate = 0.07 # Discount rate

# Stock val before earnings release
initial_stock_valuation = dcf_valuation(prior_cash_flows, discount_rate)
print(f"Initial Stock Valuation: ${initial_stock_valuation:.2f} million")

# New info - Earnings release
earnings_release = 115 # Actual earnings reported (in millions)
confidence_level = 0.5 # Confidence in the new information (0 to 1 scale)

# Update cash flows based on earnings release
updated_cash_flows = update_cash_flows_prior(prior_cash_flows, earnings_release, confidence_level)

# Recalculate stock val after earnings release
updated_stock_valuation = dcf_valuation(updated_cash_flows, discount_rate)
print(f"Updated Stock Valuation: ${updated_stock_valuation:.2f} million")

In this script:

• The dcf_valuation function calculates the present value of future cash flows.
• The update_cash_flows_prior function updates our prior beliefs about future cash flows based on the earnings release, where the confidence_level determines how much weight we give to this new information.
• We then recalculate the stock valuation using the updated cash flows.

This script is a basic representation and would be expanded with more robust Bayesian statistical methods for practical applications.

We can see here that the stock fell by about 20% after earnings (market cap of $486 million to $400 million).

Conclusion

Bayesian Efficiency offers a framework for financial decision-making.

It emphasizes the value of continuously updating beliefs and strategies based on new information.

Its implementation can be complex and requires careful consideration of initial assumptions.

Nonetheless, the Bayesian approach allows for more adaptive and informed trading and investment strategies.